正弦函数余弦函数的图象VIP免费

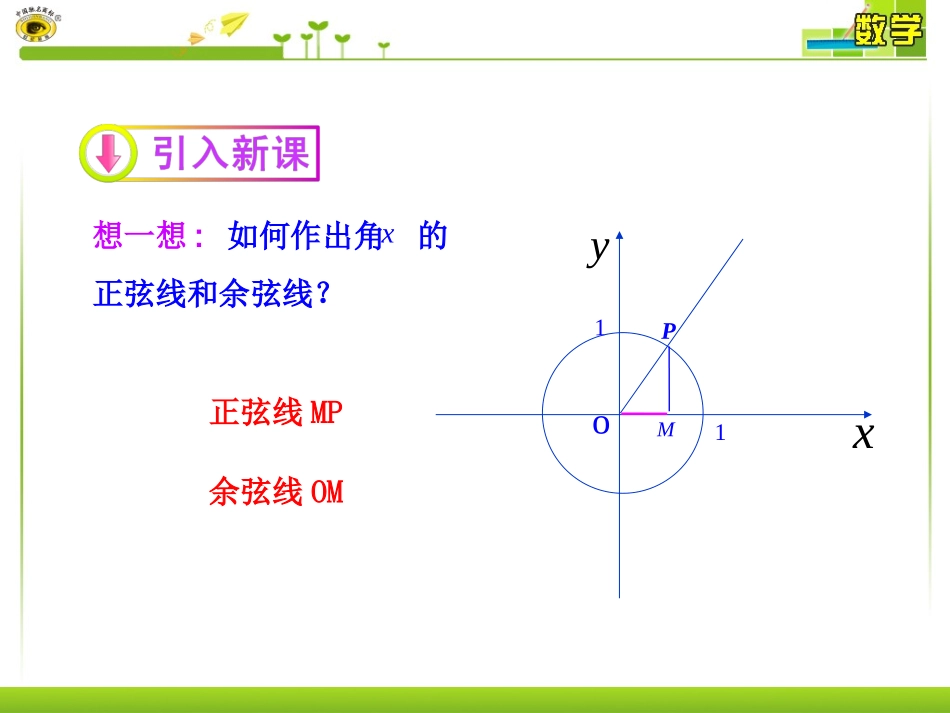
1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象Rxxy,sinRxxy,cos想一想:如何作出角的正弦线和余弦线？oxy11Mx正弦线MP余弦线OMP例如：在直角坐标系中作出点)3sin,3(ＰＭ)3sin,3(C能否借助作点Ｃ的方法作出正弦函数y＝sinx，xR∈的图象?3oxy想一想:如何利用正弦线画出的图象？sin,0,2yxxo1xyo2322667236113653435-11想一想:如何利用正弦线画出的图象？sin,0,2yxxy=sinx,x[0,2]o1o1xy2322667236113653435-1想一想:如何利用正弦线画出的图象？ysinx,x0,2y=sinx,x[0,2]o1o1xy2322667236113653435-1想一想:如何得到正弦函数的图象呢？ysinx,xR因为终边相同的角的三角函数值相同，所以的图象在…与其在4π,2π,2π,0,0,2π,2π,4π,0,2的图象形状完全一致.sinyx只需要将的图象向左、向右平移（每次个单位长度），即可得到正弦函数的图象.sin,0,2yxx2x6yo--12345-2-3-41正弦曲线想一想:如何得到正弦函数的图象呢?ysinx,xR思考：你能画出函数y=|sinx|，x∈[0，2π]的图象吗？yxOπ12π-1想一想:如何利用正弦函数的图象得到余弦函数的图象.ysinx,xRycosx,xRcosyxsin(x)2sinyx的图象的图象向左平移个单位2余弦曲线y--1-12o462462oxy---11--13232656734233561126想一想:在作正弦函数的图象时，应抓住哪些关键点？与x轴的交点)0,0()0,()0,2(图象的最高点图像的最低点)1,(23)1,2(-oxy---11--13232656734233561126想一想:在作余弦函数的图象时，应抓住哪些关键点？与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,(想一想:通过上面的分析，你能不能更快捷的画出正弦函数和余弦函数的简图？如何作？五点作图法：(1)列表(列出对图象形状起关键作用的五点坐标)(2)描点(定出五个关键点)(3)连线(用光滑的曲线顺次连接五个点)例1．画出下列函数的简图（1）y=sinx+1,x[0,2π]∈（2）y=－cosx,x[0,2π]∈解：(1)列表xxsin1sinx02232-2223211-描点作图xyo-(2)列表xxcosxcos02232010-101210110-101-1010-1-223211xyo-描点作图【变式训练】1.请补充完整下面用“五点法”作y=-sinx(0≤x≤2π)的图象时的列表.①__________；②__________；③__________.2.用“五点法”作出y=1+cosx(0≤x≤2π)的简图.x0①2π-sinx②-10③0232【典例训练】例2：1.x∈［0,2π］时，cosx<0的解集是________.2.求y=的定义域、值域.【解析】1.由y=cosx(0≤x≤2π)的图象知，cosx<0的解集是{x|