函数的概念 VIP免费

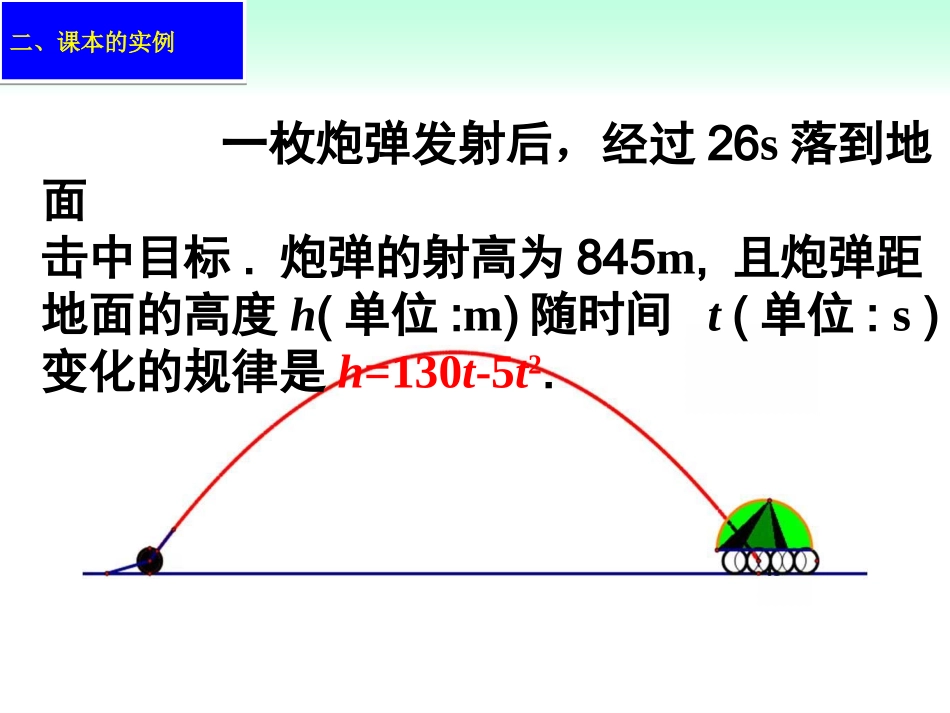
1.2.1函数的概念一、复习回顾问题１:初中我们学过哪些函数？问题２:什么叫做函数？正比例函数、反比例函数、一次函数、二次函数等简单的函数。初中对函数的定义：设在一个变化过程中有两个变量x和y，如果对于x的每一个值y都有唯一的值与它对应，那么说y是x的函数，x叫做自变量。一枚炮弹发射后，经过26s落到地面击中目标.炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是h=130t-5t2.二、课本的实例二、课本的实例时间t的变化范围是数集A={t|0≤t≤26},高度h的变化范围是数集B={h|0≤h≤845}对于数集A中的任意一个时刻t,按照对应关系h=130t-5t2,在数集B中都有惟一的高度h和它对应实例分析120011979ttA260SSB05101525203026S/106km2t/年1979818385878991939597992001下图中的曲线显示了南极上空臭氧层空洞的面积从1979～2001年的变化情况.实例分析2实例分析2二、课本的实例时间t的变化范围是数集A={t|1979≤t≤2001}面积S的变化范围是数集B={S|0≤S≤26}对于数集A中的每一个时刻t,按照图中的曲线,在数集B中都有惟一确定的臭氧层空洞面积S和它对应.“八五”计划以来我国城镇居民恩格尔系数变化情况199252.91993199919981997199619951994200050.149.948.649.946.444.541.939.21991200153.837.9时间(年)恩格尔系数(%)仿照实例(1)(2)，试描述上表中恩格尔系数和时间(年)的关系.A={1991,1992,1993,1994,1995,1996,1997,1998,1999,2000,2001}B={53.8,52.9,50.1,49.9,48.6,46.4,44.5,41.9,39.2,37.9}实例分析3实例分析3时间构成一个数集A,恩格尔系数构成一个数集B.对于数集A中的每一个时刻t,按照表中的对应值,在数集B中都有惟一确定的恩格尔系数和它对应.二、课本的实例以上三个实例有什么共同点？(2)两个数集间都有一种确定的对应关系；按照某种对应关系(3)对于数集A中的任意一个数，数集B中都有唯一确定的数和它对应.(1)都有两个非空数集A，B；记作：.:BAf你能用集合与对应的语言来刻画函数，抽象概括出函数的概念吗？不同点实例（1）是用解析式刻画变量之间的对应关系，实例（2）是用图象刻画变量之间的对应关系，实例（3）是用表格刻画变量之间的对应关系.共同点（1）都有两个非空数集（2）两个数集之间都有一种确定的对应关系对于数集A中的每一个x,按照某种对应关系f,在数集B中都有惟一确定的y和它对应,记作f:A→B.二、课本的实例三函数的概念设A,B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数,在集合B中都有唯一确定的数f(x)和它对应，那么就称为从集合A到集合B的一个函数.记作.BAf:Axxfy),(其中,x叫做自变量,x的取值范围A叫做函数的定义域.Axxf)(与x的值对应的y值叫做函数值,函数值的集合叫做函数的值域.º¯ÊýµÄ¶¨Ò壺ÉèA¡¢BÊÇÁ½¸ö·Ç¿ÕÊý¼¯£¬Èç¹û°´Ä³¸öÈ·¶¨µÄ¶ÔÓ¦¹Øϵf,ʹ¶ÔÓÚ¼¯ºÏAÖеÄÈÎÒâÒ»¸öÊýx,ÔÚ¼¯ºÏBÖж¼ÓÐΨһȷ¶¨µÄÊýf(x)ºÍËüÏà¶ÔÓ¦£¬ÄÇô¾Í³Æf:ABΪ´Ó¼¯ºÏAµ½¼¯ºÏBµÄÒ»¸öº¯Êý£¬¼Ç×÷y=f(x),x¡ÊA.ÆäÖУ¬x½Ð×ö×Ô±äÁ¿£¬xµÄÈ¡Öµ·¶Î§A½Ð×öº¯ÊýµÄ¶¨ÒåÓò£»ÓëxµÄÖµÏà¶ÔÓ¦µÄyµÄÖµ½Ð×öº¯ÊýÖµ£¬º¯ÊýÖµµÄ¼¯ºÏ{f(x)|x¡ÊA}½Ð×öº¯ÊýµÄÖµÓò.三、函数的概念：是非空数集注意唯一确定值域与集合Ｂ的关系怎样？函数的三要素：定义域、对应法则、三要素注意：1.“y=f(x)”是函数符号，可以用任意的字母表示，“y=g(x)”；4.集合B不一定是函数的值域，函数的值域是B的子集。2.函数符号“y=f(x)”中的f(x)表示与x对应的函数值，一个数，而不是f乘x．3.构成函数的三要素：定义域（集合A）、值域、对应法则（判断是否为同一函数只要看定义域、对应法则是否完全相同）。是函数吗？)R(1.1xy是函数吗？)0(.2xxy是函数吗？xxy13.3)()(图象的是的数下列图象中不能作为函xfyBxyoxyoxyoxyoBACD三、函数的概念判断下...