正切函数的图像和性质(上课用)VIP免费

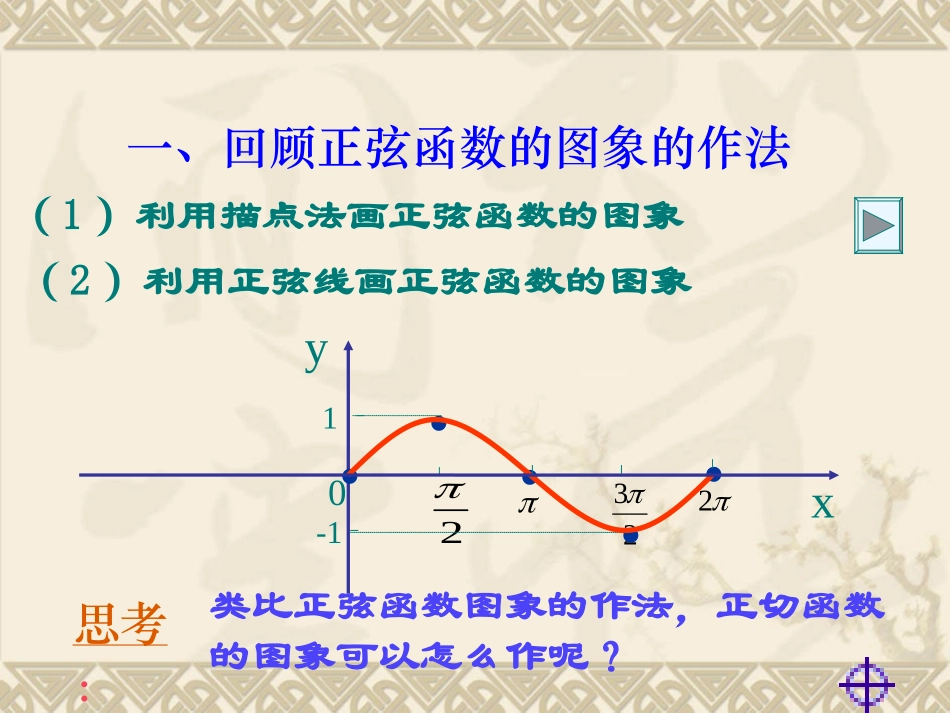
xyO(,)PxyATATOAATtan正切函数的定义：tanyxtan{|,}2yxxxkkZ正切函数的定义域：正切函数的几何表示：复习：一、回顾正弦函数的图象的作法（2）利用正弦线画正弦函数的图象（1）利用描点法画正弦函数的图象xy.023221-1....类比正弦函数图象的作法，正切函数的图象可以怎么作呢？思考：2oxy---11---1--1oA步骤:(1)等分3232656734233561126(2)作正弦线(3)平移61P1M/1p(4)连线作图过程演示二、用正切线作正切函数的图象首先我们一起分析一下正切函数y=tanx是否为周期函数？因为)tan(x（其中,Rx且Zkkx,2）)cos()sin(xxxxcossinxtan由此可知：正切函数是周期函数，π是它的一个周期，并且π是它的最小正周期.1、正切函数的周期性tan()tan,(0)xTxTtan()tanxx正切函数的周期为：2、正切函数的奇偶性tan()tanxx正切函数是奇函数类似正弦曲线的作法，我们先作正切函数在一个周期上的图象。下面我们利用正切线画出函数)2,2(,tanxxy的图象83484883xy用正切线作正切函数的图象22正切曲线的作法:1.作出坐标系及单位圆,取2.作出以上各角的正切线;3.把这些正切线移到相应的位置上,并描好点;4.用光滑的曲线连接各点,得的图象;5.由周期性,可把图象左右扩展得到正切函数的图象.83,4,8,0,8,4,83x)2,2(,tanxxy25正切函数的图象0222323xy1{|,}xxkkZ、定义域：22R、值域：3、周期性：4、奇偶性：奇函数5(,),()22kkkZ、单调性：增区间6,0),()kkZ、对称性：对称中心(2正切函数的性质：5、单调性：(,),()22kkkZ增区间：正切函数在整个定义域内是增函数吗？思考：正切函数在整个定义域内是增函数吗？答：不是.在定义域内，且，，取212145,3xxxx,tan,tan,221121xyxyxx221yy但所以不能说正切函数在整个定义域内是增函数。4531y2y例1：的定义域。求函数)4tan(xy解：的定义域是那么令ZyxZtan,4,},2{zkkzRz4x由z=,,24kxk可得的定义域是所以)4tan(xyzkkxRx,4例2：不通过求值,比较下列各组两个正切值的大小。143tan138tan)1(与)517tan()413tan()2(与27014313890是增函数，)270,90(,tanxxy143tan138tan1解：（）)413tan()2()517tan(24522，而xytan是增函数)2,2(x)517tan()413tan(tan(3)4)523tan(2tan()5143tan138tan)1(与)517tan()413tan()2(与tan()4例2：不通过求值,比较下列各组两个正切值的大小。课堂小结：正切函数的图象1{|,}xxkkZ、定义域：22R、值域：3、周期性：4、奇偶性：奇函数5(,),()22kkkZ、单调性：增区间6,0),()kkZ、对称性：对称中心(2作业：