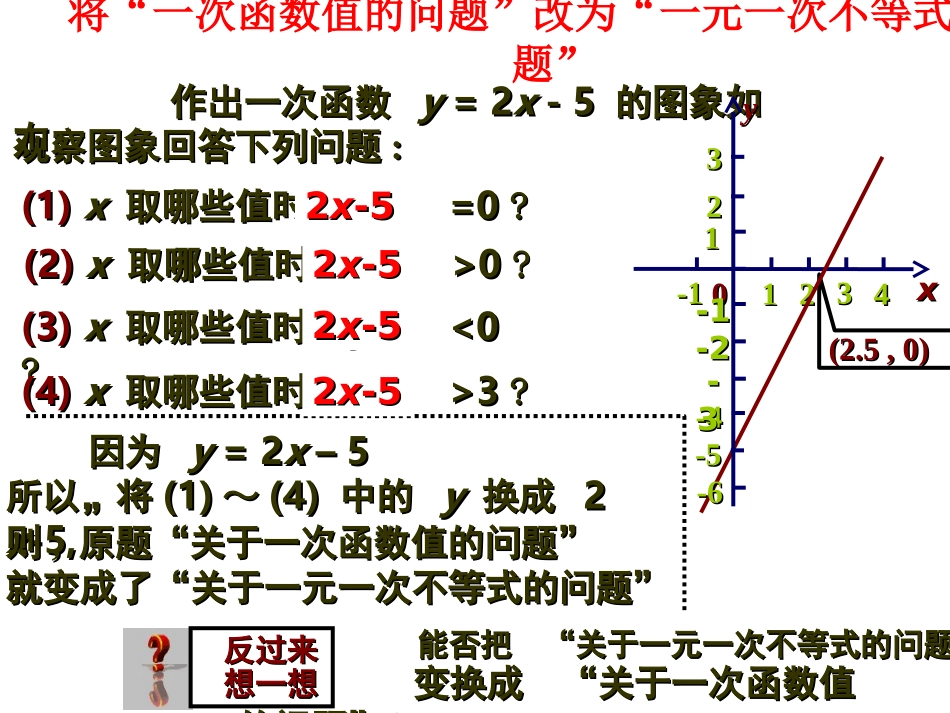
•第一章第五节一元一次不等式与一次函数(1)2013年2月28日星期四我们知道,我们知道,一次函数的图象是一条直线。一次函数的图象是一条直线。作出一次函数作出一次函数yy=2=2xx--55的图象如右,的图象如右,(2.5,0)(2.5,0)观察图象回答下列问题观察图象回答下列问题::回顾与思考回顾与思考(1)(1)xx取哪些值时取哪些值时,,yy=0=0??(2)(2)xx取哪些值时取哪些值时,,yy>0>0??xx>2.5>2.5时时,,yy>>0;0;xx=2.5=2.5时时,,yy==0;0;(3)(3)xx取哪些值时取哪些值时,,yy<0<0??xx<2.5<2.5时时,,yy<<0;0;(4)(4)xx取哪些值时取哪些值时,,yy>3>3??xx>4>4时时,,yy>3>3;;思考思考能否将上述“关于函数值的问题”能否将上述“关于函数值的问题”,,改为“关于改为“关于xx的不等式的问题”的不等式的问题”??00xx112233-1-14411-1-1-2-233-4-4-3-322-5-5-6-6yy将“一次函数值的问题”改为“一元一次不等式的问题”作出一次函数作出一次函数yy=2=2xx--55的图象如的图象如右,右,观察图象回答下列问题观察图象回答下列问题::(1)(1)xx取哪些值时取哪些值时,,yy=0=0??(2)(2)xx取哪些值时取哪些值时,,yy>0>0??(3)(3)xx取哪些值时取哪些值时,,yy<0<0??(4)(4)xx取哪些值时取哪些值时,,yy>3>3??(2.5,0)(2.5,0)yy00xx112233-1-14411-1-1-2-233-4-4--3322-5-5-6-6因为因为yy=2=2xx––55,,所以,将所以,将(1)(1)~~(4)(4)中的中的yy换成换成22xx--5,5,22xx--5522xx--5522xx--5522xx--55则则,,原题“关于一次函数值的问题”原题“关于一次函数值的问题”就变成了“关于一元一次不等式的问题”就变成了“关于一元一次不等式的问题”反过来反过来想一想想一想能否把“关于一元一次不等式的问题”能否把“关于一元一次不等式的问题”变换成“关于一次函数值变换成“关于一次函数值的问题”的问题”??由上述讨论易知:由上述讨论易知:函数、(方程)不等式““关于一次函数的值的问题”关于一次函数的值的问题”可变换成“关于一元一次不等式的问题”;可变换成“关于一元一次不等式的问题”;反过来,反过来,“关于一元一次不等式的问题”“关于一元一次不等式的问题”可变换成“关于一次函数的值的问题”可变换成“关于一次函数的值的问题”。。因此,因此,我们既可以运用函数图象解不等式,我们既可以运用函数图象解不等式,也可以运用解不等式帮助研究函数问题,也可以运用解不等式帮助研究函数问题,二者相互渗透,互相作用。二者相互渗透,互相作用。我们既可以运用函数图象解不等式,我们既可以运用函数图象解不等式,也可以运用解不等式帮助研究函数问题,也可以运用解不等式帮助研究函数问题,二者相互渗透,互相作用。二者相互渗透,互相作用。不等式与函数、方程是紧密联系着不等式与函数、方程是紧密联系着的一个整体。的一个整体。不等式与函数、方程是紧密联系着不等式与函数、方程是紧密联系着的一个整体。的一个整体。如果如果yy=-=-2x2x--55,,那么当那么当xx取何值时取何值时,,yy>0>0??你解答此道题你解答此道题,,可有几种方法可有几种方法??想一想想一想法一法一::将函数问题转化为不等式问题将函数问题转化为不等式问题..即即解不等式解不等式--2x2x--55>0>0;;法二法二::图象法。图象法。xxyy--11--22--33--44--5511--11--22--33--44--55--66112233由图易知,由图易知,当当xx<-2.5<-2.5时时yy>>0.0.用“函数图象法”及“解不等式法”解函数用“函数图象法”及“解不等式法”解函数问题问题做一做兄弟俩赛跑,哥哥先让弟弟跑9m,然后自已才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.列出函数关系式,作出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?(4)你是怎样求解的?与同伴交流.解:设哥哥起跑后所用的时间为x(s).哥哥跑过的距离为y1(m)弟弟跑过的距离为y2(m).则哥哥与弟弟每人所跑的距离y(m)与时间x(s)之间的函数关系式分别是:y1=4xy2=3x+9(1)_______________时,弟弟跑在哥哥前面.(2)__________时,哥哥跑在弟弟前面.(3)______先跑过20m.______先跑过100m.(4)你是怎样求解的?与同伴交流.思路一:图象法0(s)9(s)y1=...