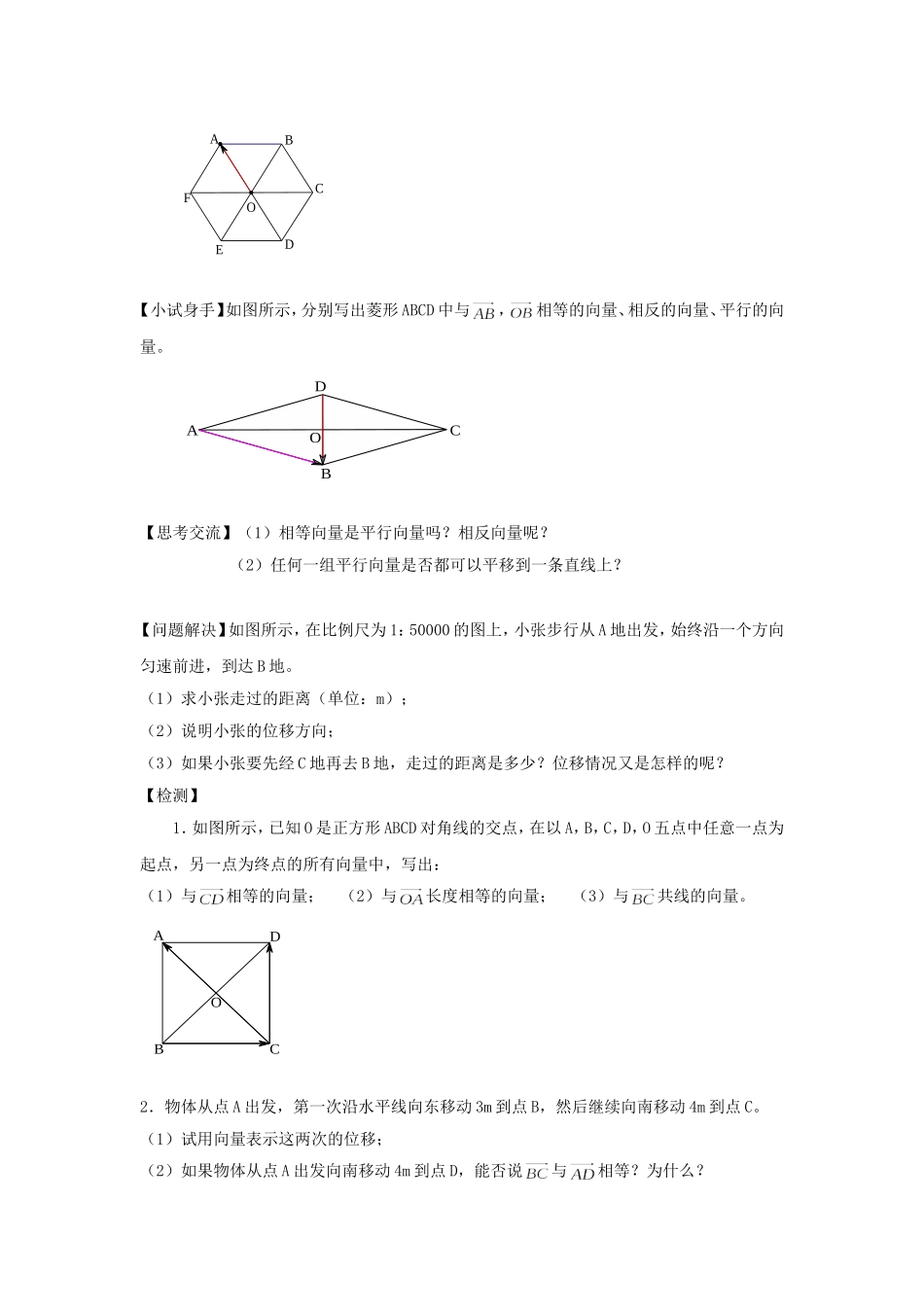
平面向量的概念(2)【教学目标】知识与技能:理解相等向量、相反向量、平行向量的概念。过程与方法:通过生活中与向量有关的实例进行引入,使数学与生活紧密联系,让学生感受平面向量的“数”与“形”。通过自主实践、相互交流、合作探究等手段,培养学生的逻辑思维能力。情感、态度及价值观:通过探究、观察、实践等方法,让学生发现向量在现实生活中的意义和作用,激发学生学习向量的兴趣与热情。【教学重点、难点】教学重点:理解相等向量、相反向量、平行向量的概念。教学难点:理解相等向量、相反向量、平行向量的概念。【教学方法】教学方法:自主实践、相互交流、合作探究【教学过程】一.情境引入:1.回顾旧知:(1)什么是向量?向量应如何表示?(2)什么是向量的模?2.合作探究:为达成《国家体育锻炼标准测试项目表》中的训练要求,体育课上老师对学生进行50(252往返跑)测试。学生甲、乙两人为一组分别从起点A、B跑到50处C、D后折返跑回到A、B点。(1)每个人从起点跑到折返处,再从折返处跑回起点(终点)所发生的位移分别是哪些?试用向量表示出来。(2)表示从点A到点C所发生的位移的向量与表示从点B到点D所发生的位移的向量有什么关系?(3)表示从点A到点C所发生的位移的向量与表示从点C到点A所发生的位移的向量有什么关系?二.新授:1.相等向量:长度相等且方向相同的向量叫做相等向量(或同一向量)。向量与相等,记作:。2.相反向量:长度相等且方向相反的向量叫做相反向量。向量与相反,记作:。3.平行向量:如果两个非零向量方向相同或相反,我们就说这两个向量互相平行,叫做平行向量或共线向量。向量向量与平行,记作:。规定:零向量与任何向量平行,即。【试试看】判断下列说法是否正确,并说明理由。(1)若,则;(2)如果两个向量相等,那么它们的起点相同,终点相同;(3)模相等的两个平行向量是相等的向量;(4)两个相等向量的模相等;(5)平行向量一定方向相同;(6)不相等的向量一定不平行;(7)若四边形ABCD是平行四边形,则。【例1】如图所示,在4×5方格纸中有一个向量,分别以图中的格点为起点和终点作向量,其中与相等的向量有多少个?与长度相等且共线的向量有多少个?(除外)BA【小试身手】如图所示,在3×4方格纸中有一个向量,分别以图中的格点为起点和终点作向量,其中与相等的向量有多少个?与长度相等且共线的向量有多少个?(除外)BA【例2】如图所示,设O是正六边形ABCDEF的中心,分别写出与相等的向量、相反的向量、平行的向量。OEDCBFA【小试身手】如图所示,分别写出菱形ABCD中与,相等的向量、相反的向量、平行的向量。ODCBA【思考交流】(1)相等向量是平行向量吗?相反向量呢?(2)任何一组平行向量是否都可以平移到一条直线上?【问题解决】如图所示,在比例尺为1:50000的图上,小张步行从A地出发,始终沿一个方向匀速前进,到达B地。(1)求小张走过的距离(单位:m);(2)说明小张的位移方向;(3)如果小张要先经C地再去B地,走过的距离是多少?位移情况又是怎样的呢?【检测】1.如图所示,已知O是正方形ABCD对角线的交点,在以A,B,C,D,O五点中任意一点为起点,另一点为终点的所有向量中,写出:(1)与相等的向量;(2)与长度相等的向量;(3)与共线的向量。ODCBA2.物体从点A出发,第一次沿水平线向东移动3m到点B,然后继续向南移动4m到点C。(1)试用向量表示这两次的位移;(2)如果物体从点A出发向南移动4m到点D,能否说与相等?为什么?三.小结:四.作业:1.设O是正三角形ABC的中心,则向量,,是()A.相等向量B.模相等的向量C.共线向量D.共起点的向量CBOA2.如图所示,设O是等腰梯形ABCD中两条对角线AC与BD的交点,分别写出与,,相等的向量、相反的向量、共线的向量。ODCBA平行向量(或共线向量)相等向量相反向量