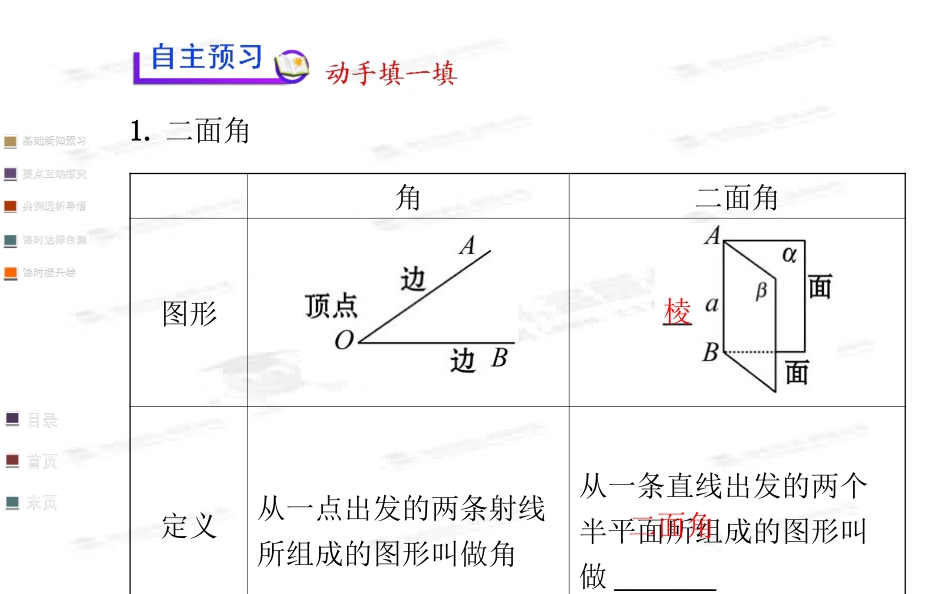
2.3.2平面与平面垂直的判定1.“”“”“使学生正确理解和掌握二面角二面角的平面角及直二”“”面角两个平面互相垂直的概念.2.使学生掌握两个平面垂直的判定定理及其简单应用.1.二面角角二面角图形定义从一点出发的两条射线所组成的图形叫做角从一条直线出发的两个半平面所组成的图形叫做_______棱二面角角二面角构成——边点边(顶点)——面直线面(棱)表示法∠AOB二面角________或二面角_________α-a-βα-AB-β2.二面角的平面角(1)满足条件:如图,二面角α-l-β的平面角为∠AOB,则平面角∠AOB应满足的条件为:①____;②_____;③_____.O∈lOA⊥lOB⊥l(2)直二面角:若二面角α-l-β的平面角∠AOB=90°,则该二面角叫做_________.(3)表示方法:图中二面角可记为二面角_______或_____.直二面角α-l-βP-l-Q3.平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是_________,就说这两个平面互相垂直.(2)表示:平面α与平面β垂直记作:_______.直二面角α⊥β4.平面与平面垂直的判定定理(1)文字语言:若一个平面过另一个平面的_____,则这两个平面_________.(2)符号语言:____________⇒α⊥β.(3)图形语言:垂线互相垂直a⊂α,a⊥β1.“”判一判理清知识的疑惑点(“√”正确的打,错误的打“×”).(1)两个相交平面组成的图形叫做二面角.()(2)二面角的平面角是从棱上一点出发,分别在两个面内所作射线所成角的最小角.()(3)若平面α⊥平面β,则α内的所有直线都与β垂直.()(4)若平面α和平面β不垂直,则平面α内所有直线与β都不垂直.()提示:(1)错误.由二面角的定义:从一条直线出发的两个半平面所组成的图形叫做二面角,所以(1)不对,实质上它共有四个二面角.(2)错误.平面内所作的射线不一定垂直于二面角的棱,故不对.(3)错误.例如,正方体ABCD-A1B1C1D1中,平面ABCD与平面ABB1A1垂直,但平面ABCD内的直线AC与平面ABB1A1不垂直,所以错误.(4)正确.假设在α内存在直线与β垂直,由面面垂直的判定定理知α⊥β,与α,β不垂直矛盾.答案:(1)×(2)×(3)×(4)√2.“”练一练尝试知识的应用点(请把正确的答案写在横线上).(1)下图给出的二面角表示为,二面角的平面角是.(2)过平面α的一条垂线可作个平面与平面α垂直,过平面α的一条斜线,可作个平面与平面α垂直.(3)如图所示:在正方体ABCD-A1B1C1D1中:①二面角A1-AB-D的大小为:;②二面角D1-AB-D的大小为:;③二面角D1-BC-D的大小为.【解析】(1)根据二面角的表示法表示为α-l-β,平面角是∠AOB.答案:α-l-β∠AOB(2)只要过垂线的平面都和该平面垂直,故可作无数多个;过斜线上一点,只能作一条平面的垂线,斜线和垂线确定一个平面,故过平面的一条斜线,只能作一个平面的垂面.答案:无数1(3)①显然为直二面角,②∠D1AD为二面角的平面角,为45°,③∠D1CD为二面角的平面角,为45°.答案:90°45°45°一、二面角及其平面角根据如图所示的二面角及其平面角,探究下列问题:探究1:二面角的平面角所确定的平面和二面角的棱的关系?提示:二面角的平面角所确定的平面和二面角的棱垂直.探究2:对于确定的二面角而言,满足上述特点的平面角有多少个?请在二面角上任意作两个平面角,平面角的大小与顶点在棱上的位置有无关系?提示:满足上述特点的平面角有无数多个,平面角的大小与顶点在棱上的位置无关,只与二面角的张角大小有关.如图所示.【探究提升】二面角及其平面角的三个关注点(1)二面角是一个空间图形,由两个半平面构成;二面角的平面角是一个平面图形.(2)二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多大的二面角,平面角是直角的二面角叫做直二面角.(3)二面角的平面角的特点①二面角的平面角的范围是[0,π].②二面角的平面角的大小与顶点O的位置无关.③平面角的顶点在棱上,两边分别在二面角的两个半平面内,两边分别垂直于棱.【拓展延伸】二面角的平面角的三种作法(1)定义法:在二面角的棱上任找一点,在两个半平面内分别作垂直于棱的射线.如图∠AOB即为二面角的平面角.(2)垂面法:过棱上一点作与棱垂直的平面,该平面与二面角的两个半平面相交,得两条交线,这两条交线所成的角即为二面角的平面角.如图∠AOB即为二面角的平面角.(3)垂线...