离散数学第6章作业答案 VIP免费

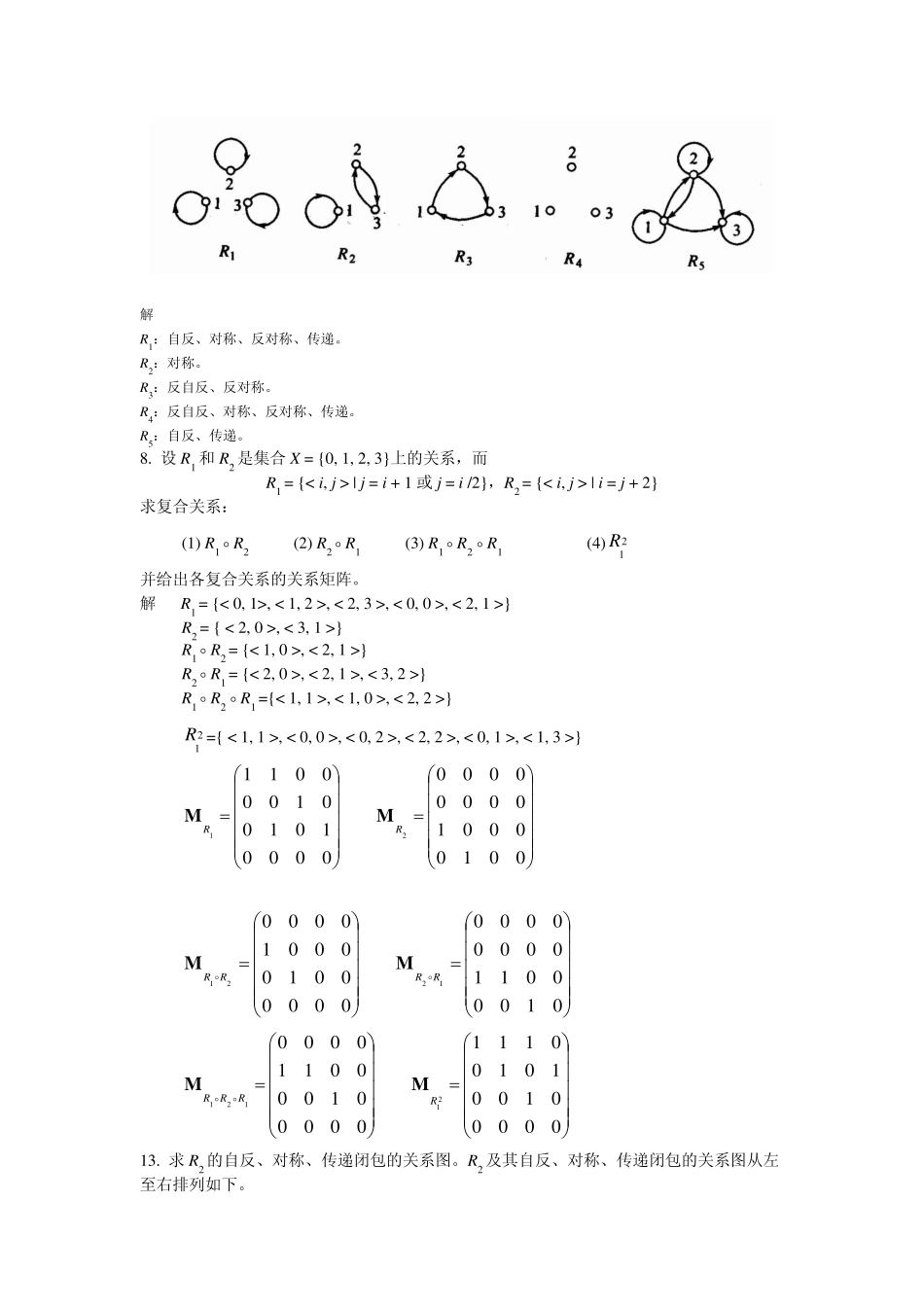
第六章习题答案2.设P={<1,2>,<2,4>,<3,3>}，Q={<1,3>,<2,4>,<4,2>}找出PQ,PQ,dom(P),dom(Q),ran(P)及ran(Q)，并证明：dom(PQ)=dom(P)dom(Q)ran(PQ)ran(P)ran(Q)解PQ={<1,2>,<2,4>,<3,3>,<1,3>,<4,2>}，PQ={<2,4>}dom(P)={1,2,3}，dom(Q)={1,2,4}，ran(P)={2,3,4}，ran(Q)={2,3,4}。xdom(PQ)y(PQ)y(PQ)y(P)y(Q)xdom(P)xdom(Q)xdom(P)dom(Q)yran(PQ)x(PQ)x(PQ)x(P)x(Q)yran(P)yran(Q)yran(P)ran(Q)如上例，ran(PQ)={4}{2,3,4}=ran(P)ran(Q)3.若关系R和S自反的，对称的和传递的，证明：RS也是自反的，对称的和传递的。证明设R和S是集合A上的关系。因为R和S是自反的，所以，对于A中的任意元素x，有R和S。因此RS，即RS是自反的。因为R和S是对称的，所以对于任意，RSRSRSRS因此，RS是对称的。因为R和S是传递的，所以对于任意和，RSRSRSRS(RR)(SS)RSRS因此，RS是传递的。5．设A={1,2,3}，A上的关系R1,R2,R3,R4,R5分别由图6.17给出，试问：R1,R2,R3,R4,R5各有哪些性质？解R1：自反、对称、反对称、传递。R2：对称。R3：反自反、反对称。R4：反自反、对称、反对称、传递。R5：自反、传递。8.设R1和R2是集合X={0,1,2,3}上的关系，而R1={|j=i+1或j=i/2}，R2={|i=j+2}求复合关系：(1)R1R2(2)R2R1(3)R1R2R1(4)21R并给出各复合关系的关系矩阵。解R1={<0,1>,<1,2>,<2,3>,<0,0>,<2,1>}R2={<2,0>,<3,1>}R1R2={<1,0>,<2,1>}R2R1={<2,0>,<2,1>,<3,2>}R1R2R1={<1,1>,<1,0>,<2,2>}21R={<1,1>,<0,0>,<0,2>,<2,2>,<0,1>,<1,3>}0010000100000000000010100100001121RRMM010000110000000000000010000100001221RRRRMM0000010010100111000001000011000021121RRRRMM13.求R2的自反、对称、传递闭包的关系图。R2及其自反、对称、传递闭包的关系图从左至右排列如下。14.令R1,R2是集合A上的二元关系，并设R1R2，试证明下列关系式。(3)t(R1)t(R2)证明R1R2t(R2)，t(R2)是包含R1的传递关系，由传递闭包定义知道，t(R1)是包含R1的最小传递关系，所以，t(R1)t(R2)。15.设R1,R2是A上的二元关系，试证明(3)t(R1R2)t(R1)t(R2)并用反例说明t(R1R2)=t(R1)t(R2)不一定成立。证明因为R1R1R2，所以t(R1)t(R1R2)。因为R2R1R2，所以t(R2)t(R1R2)。因此，t(R1)t(R2)t(R1R2)。令A={1,2}，R1={<1,2>}，R2={<2,1>}。因为R1是传递的，故t(R1)=R1。因为R2是传递的，故t(R2)=R2。因此，t(R1)t(R2)=R1R2={<1,2>,<2,1>}，而t(R1R2)={<1,2>,<2,1>,<1,1>,<2,2>}。18.对于下列集合上的整除关系，画出哈斯图。(1)A={1,2,3,4,6,8,12,24}(2)B={1,2,3,…,12}(1){2,3,4}没有最大元、最小元，极大元为3和4，极小元为2和3，上界为12和24，上确界为12，下界为1，下确界为1。(2){2,3,4}没有最大元、最小元，极大元为3和4，极小元为2和3，上界为12，上确界为12，下界为1，下确界为1。20.图6.21上给出了集合A={1,2,3,4}上的四个偏序关系，试画出它们的哈斯图。并判别哪一个是全序或良序关系。1213264824481263712510911(a)去掉关系图中的自环，没有进入顶点4的有向边，将4画在最下面，去掉从4发出的有向边，没有进入顶点1的有向边，将1画在第二层，去掉从1发出的有向边，剩下两个孤立点2和3，将2和3画在最上面。连接4和1，1和2，1和3，得到哈斯图。23.令T是笛卡尔平面RR上的关系，T的定义如下：T当且仅当x1x2y1y2请据此判断下面哪个断言是真哪个是假，如果断言是假，说明理由。(1)T是偏序的。(2)T是线序的。(3)T是良序的。答T是偏序，不是线序，更不是良序。<0,1>和<1,0>不可比。4441111223333422