弧弦圆心角弦心距VIP免费

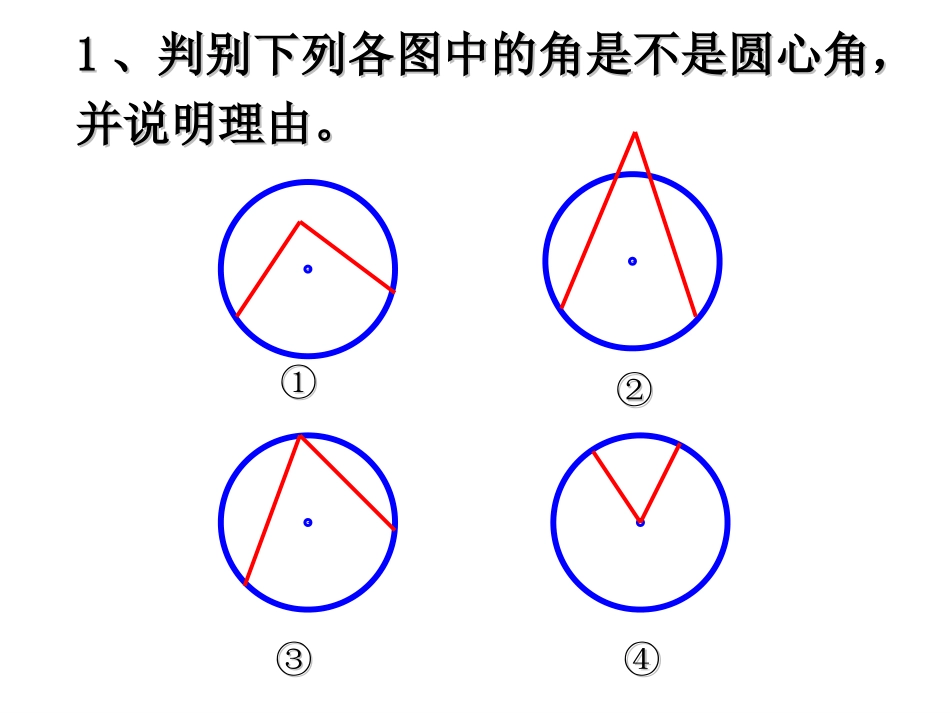
24．1．3弧、弦、圆心角圆心角所对的弧为AB，AOB过点O作弦AB的垂线,垂足为M,OABM顶点在圆心的角,叫圆心角，如,AOB所对的弦为AB；图1则垂线段OM的长度,即圆心到弦的距离，叫弦心距,图1中，OM为AB弦的弦心距。点击概念11、判别下列各图中的角是不是圆心角，、判别下列各图中的角是不是圆心角，并说明理由。并说明理由。①①②②③③④④2、下列图中弦心距做对了的是（）┐┐①②③④3、下面我们一起来观察一下：在⊙O中有哪些圆心角？并说出圆心角所对的弧，弦。ABCo如图，将圆心角∠如图，将圆心角∠AOBAOB绕圆心绕圆心OO旋旋转到∠转到∠A’OB’A’OB’的位置，你能发现哪些等量关的位置，你能发现哪些等量关系？为什么？系？为什么？·OAB知识探究知识探究·OABA′B′A′B′∠AOB=A’OB’,∠AB=A’B’,AB=A’B’,这样，我们就得到下面的定理：定理·OAA′B′B圆心角定理：相等的圆心角所对的弧相等，所对的弦相等，所对弦的弦心距也相等。在同圆或等圆中，由条件:①∠AOB=A′O′B′∠②AB=A′B′⌒⌒③AB=A′B′可推出如图:∠AOB＝∠COD,那么吗?AB=CD⌒⌒ＡＢＣＤOEF思考:如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么___________，_________________．（2）如果，那么____________，_____________．（3）如果∠AOB=COD∠，那么_____________，_________．（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？·CABDEFOAOBCODAB=CDAOBCOD,,11,22ABCDAECFOAOCR.OEOFOEABOFCDAEABCFCDtAOERtCOFOEOF证明：又＝＝又＝AB=CD练习ABCDABCDABCD在同圆或等圆中如果弦相等那么弦所对的圆心角相等弦所对的弧相等弦的弦心距相等在同圆或等圆中如果弦心距相等那么弦心距所对应的圆心角相等弦心距所对应的弧相等弦心距所对应的弦相等在同圆或等圆中如果弧相等那么弧所对的圆心角相等弧所对的弦相等弧所对的弦的弦心距相等延伸圆心角定理及推论整体理解：圆心角定理及推论整体理解：(1)圆心角(2)弧(3)弦(4)弦心距知一得三OαAA′B′αB判断：1、等弦所对的弧相等。（）2、等弧所对的弦相等。（）3、圆心角相等，所对的弦相等。(）4、弦相等，所对的圆心角相等。（）×××√证明：∵∴AB=AC,△ABC等腰三角形．又∠ACB=60°，∴△ABC是等边三角形，AB=BC=CA.∴∠AOB＝∠BOC＝∠AOC.·ABCO例题例1如图在⊙O中，，∠ACB=60°，求证∠AOB=∠BOC=∠AOC.AB=AC⌒⌒AB=AC⌒⌒1.如图，AB是⊙O的直径，∠COD=35°求∠AOE的度数．·AOBCDEBOC=COD=DOE=35180335AOE75解：BC=CD=DE⌒⌒⌒BC=CD=DE⌒⌒⌒∵随堂训练DCABO2、如图，已知AB、CD为的两条弦，求证AB＝CD.AD=BC⌒⌒⊙O随堂训练例2：已知如图（1）⊙O中，AB、CD为⊙O的弦，∠1=∠2，求证：AB=CD变式练习1：如图（1），已知弦AB=CD，求证：∠1=∠212ABCDO（1）变式练习2：如图（2），⊙O中，弦AB=CD，求证：BD=ACABCDO变式练习3：如图（2），⊙O中，弦BD=AC，猜测∠A与∠D的数量关系。（２）OBCAE3、如图，BC为⊙O的直径，OA是⊙O的半径，弦BEOA∥。求证：AC=AE⌒⌒MNOBAC如图，已知OA、OB是⊙O的半径，点C为AB的中点，M、N分别为OA、OB的中点，求证：MC=NC⌒