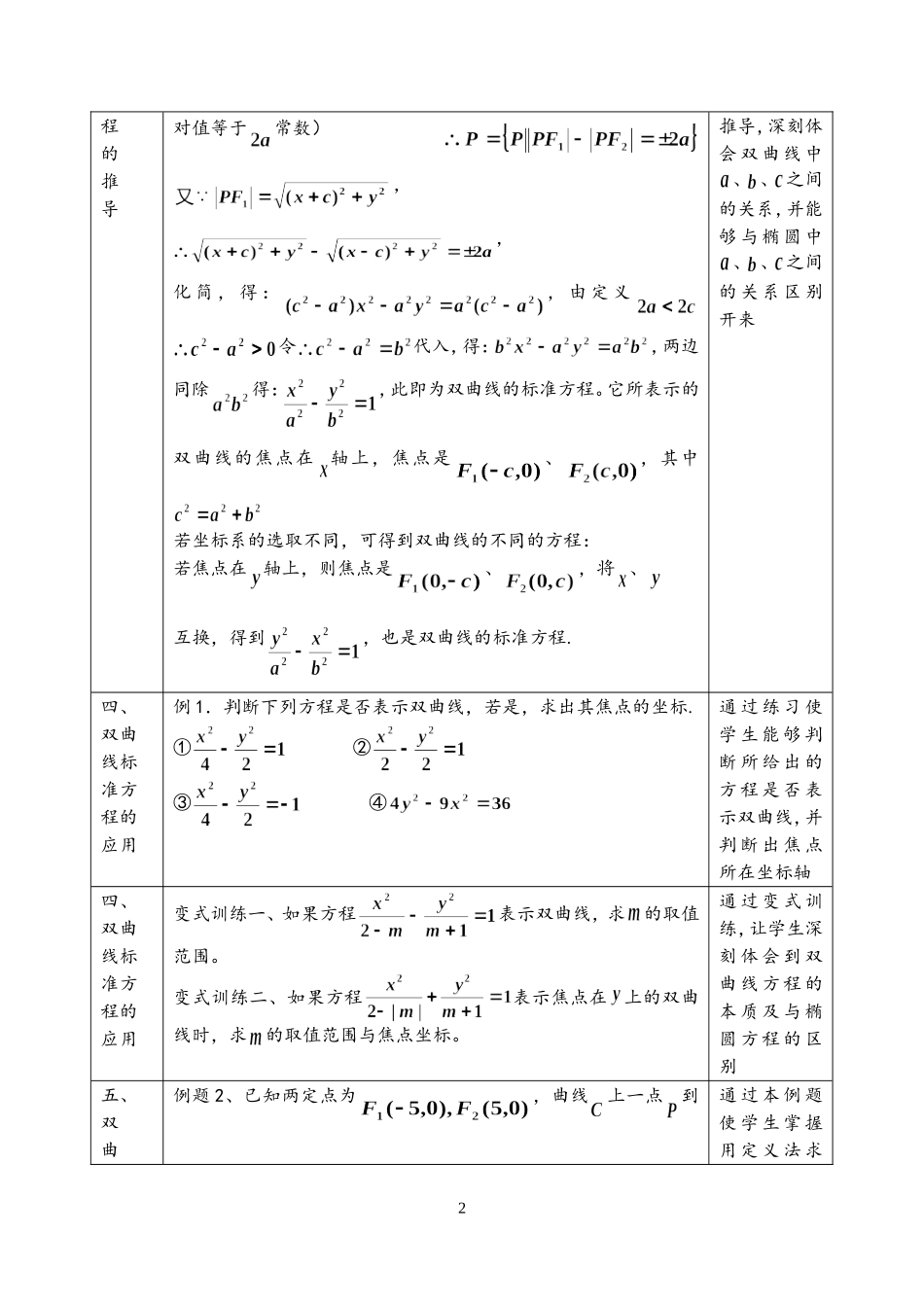
双曲线及其标准方程的教学设计一、教学目标:1.掌握双曲线的定义;2.推导双曲线的标准方程;3.掌握两类标准方程,会求双曲线的方程;二、教学重点:双曲线的定义及应用三、教学难点:(1)推导双曲线的方程;(2)双曲线方程的应用与求解四、教学过程:活动环节教学过程设计意图一、复习与回顾1、复习椭圆的定义(注意:1、定义中这一条件);2、椭圆的标准方程及、、之间的关系或()焦点回顾旧知识,为双曲线内容的学习作准备二、双曲线的定义1.演示拉链实验,让学生自己总结出双曲线的定义;2.要注意双曲线定义的条件、绝对值;3.要注意对;,等情况的讨论;注意:①在条件下:时为双曲线的一支(含的一支);时为双曲线的另一支(含的一支)②当时,表示两条射线.③当时,不表示任何图形.④两定点、叫做双曲线的焦点,叫做焦距.4.观察生活中的双曲线现象,深化理解双曲线的定义。根据实验过程与结果,引导学生抓住作图的关键(点与距离),让学生对照椭圆的定义,鼓励用自己的语言概括定义。自主得出双曲线的定义,并讨论条件发生改变时,方程所对应的曲线的变化。三、双曲线标准方标准方程的推导:1、建;2、列;3、化取过焦点的直线为轴,线段的垂直平分线为轴。设为双曲线上的任意一点,双曲线的焦距是.则:、,又设与距离之差的绝让学生熟悉推导曲线方程的一般过程,同时培养学生自主运算、化简的能力;通过体验1程的推导对值等于常数),,化简,得:,由定义令代入,得:,两边同除得:,此即为双曲线的标准方程。它所表示的双曲线的焦点在轴上,焦点是、,其中若坐标系的选取不同,可得到双曲线的不同的方程:若焦点在轴上,则焦点是、,将、互换,得到,也是双曲线的标准方程.推导,深刻体会双曲线中、、之间的关系,并能够与椭圆中、、之间的关系区别开来四、双曲线标准方程的应用例1.判断下列方程是否表示双曲线,若是,求出其焦点的坐标.①②③④通过练习使学生能够判断所给出的方程是否表示双曲线,并判断出焦点所在坐标轴四、双曲线标准方程的应用变式训练一、如果方程表示双曲线,求的取值范围。变式训练二、如果方程表示焦点在上的双曲线时,求的取值范围与焦点坐标。通过变式训练,让学生深刻体会到双曲线方程的本质及与椭圆方程的区别五、双曲例题2、已知两定点为,曲线上一点到通过本例题使学生掌握用定义法求2线标准方程与定义应用的距离的差的绝对值等于6,求曲线的标准方程.练习:1.已知是椭圆的两个焦点,平面内一个动点满足,则动点的轨迹是()A.双曲线B.双曲线的一个分支C.两条射线D.一条射线2.过双曲线左焦点的直线交双曲线的左支于、两点,为其右焦点,则_____解双曲线的方程,两个练习主要是针对双曲线定义的应用来设置的,让学生进一步理解双曲线的定义,并能够灵活应用六、求解双曲线的方程例题3、求经过点A(2,5)且a=,焦点在Y轴上的双曲线的标准方程。练习:已知动圆过定点与圆内切,求动圆圆心的轨迹方程.进一步强化曲线方程的求解;强化化简能力七、走向高考1.若双曲线上的点P到点(5,0)的距离是15,则点P到点(-5,0)的距离是()A.7B.23C.5或25D.7或232.设是双曲线的两个焦点,点在双曲线上,且,求的面积_______机动处理,旨在加深学生对双曲线定义的理解与应用;以高考的标准来检测本节课的学习效果八、小结与作业1.小结(1)双曲线的定义;(2)双曲线的标准方程;(3)双曲线标准方程与定义的应用2.作业:P55练习第1,2题P61习题A第1、2、3题回顾本节课的内容;布置作业,巩固学习效果3