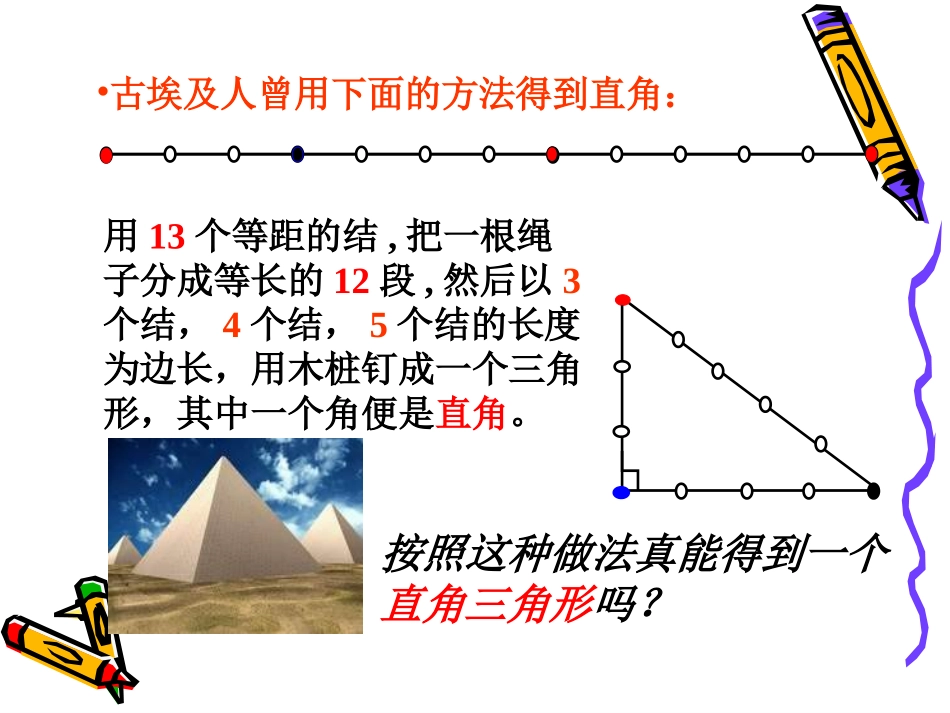
皇路店一初中吴娟直角三角形有哪些性质?(1)有一个角是直角;(2)两个锐角的和为90°(互余);(3)两直角边的平方和等于斜边的平方(勾股定理)反之,一个三角形满足什么条件才能是直角三角形呢?温故知新按照这种做法真能得到一个直角三角形吗?•古埃及人曾用下面的方法得到直角:用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。学习目标:1、熟记:勾股定理的逆定理(重点)(直角三角形的判定定理)2、运用:勾股定理的逆定理,(难点)判定一个三角形是直角三角形并解决实际问题。一、设疑自探(学而不疑则怠,疑而不探则空)请同学们结合P112-114内容,围绕学习目标,提出自己心中的疑问。1、勾股定理逆定理的内容2、判定一个三角形是直角三角形的方法有哪些?(从角、三角形全等和三边关系这三个方面总结)3、画出三边长度分别为如下数据的三角形,并用量角器测量,判断哪些图形是直角三角形?(1)a=3,b=4,c=5;(2)a=4,b=6,c=8;(3)a=6,b=8,c=10;若三角形三边a,b,c(c为最长边),会出现什么三角形,各自满足怎样的关系式?4、勾股定理和它的逆定理之间的关系?5、勾股数的概念,常用的勾股数有哪些?自探提示:二、解疑合探(独学而无友,则孤陋而寡闻)合探提示:1、将你的自学成果放在小组内统一一下2、将你在自探过程中不能独立解决的问题放在小组中交流一下3、组长做好分工和记录展示与评价分工表题号展示小组展示方式评价小组12板书826口头133板书745口头451板书6展示要求:1、口头展示声音洪亮吐字清晰。2、不仅展示结果还要有方法总结。评价要求:1、声音洪亮有“教态”2、重点点评优缺点及方法总结3、非点评同学认真倾听,有疑问或见解及时提出4、对展示同学打分如果三角形的三边长a、b、c满足,那么这个三角形是直角三角形。a2+b2=c2问题1、勾股定理逆定理1、定义法:证明三角形的一个角是直角(两个内角互余)2、三角形全等:证明两个三角形全等,且其中一个是直角三角形3、勾股定理逆定理:证明两边的平方和等于第三边的平方问题2、判定一个三角形是直角三角形的方法直角三角形钝角三角形锐角三角形a2+b2=c2a2+b2c2问题3、若规定三角形三边长a,b,c(c为最长边),会出现什么三角形,各自满足怎样的关系式?勾股定理:如果直角三角形两直角边分别为a,b,斜边为c,那么.a2+b2=c2勾股定理的逆定理:如果三角形的三边长a、b、c满足,那么这个三角形是直角三角形.a2+b2=c2互逆问题4、勾股定理和它的逆定理之间的关系能够成为直角三角形三条边长的三个正整数,称为勾股数.常用的勾股数有:3,4,56,8,105,12,13······问题5、勾股数的概念,常用的勾股数三、质疑再探(疑是开山斧,探是深耕犁)随着对本节知识的理解,你又产生了哪些新的疑惑呢?请大胆提出,我们共同探讨。现在你知道古埃及人画直角的道理吗?解:设每两个结间的距离为a,则AC=3a,AB=4a,BC=5a∵AC2+AB2=(3a)2+(4a)2=25a2BC2=(5a)2=25a2∴AC2+AB2=BC2△ABC是直角三角形,且∠A是直角四、运用拓展•根据本节课的学习内容,请你来当小老师,自编1—3道习题,考考大家吧!已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.ABCD3412135∟直击中招感谢各位同学精彩配合!恳请各位领导批评指正!