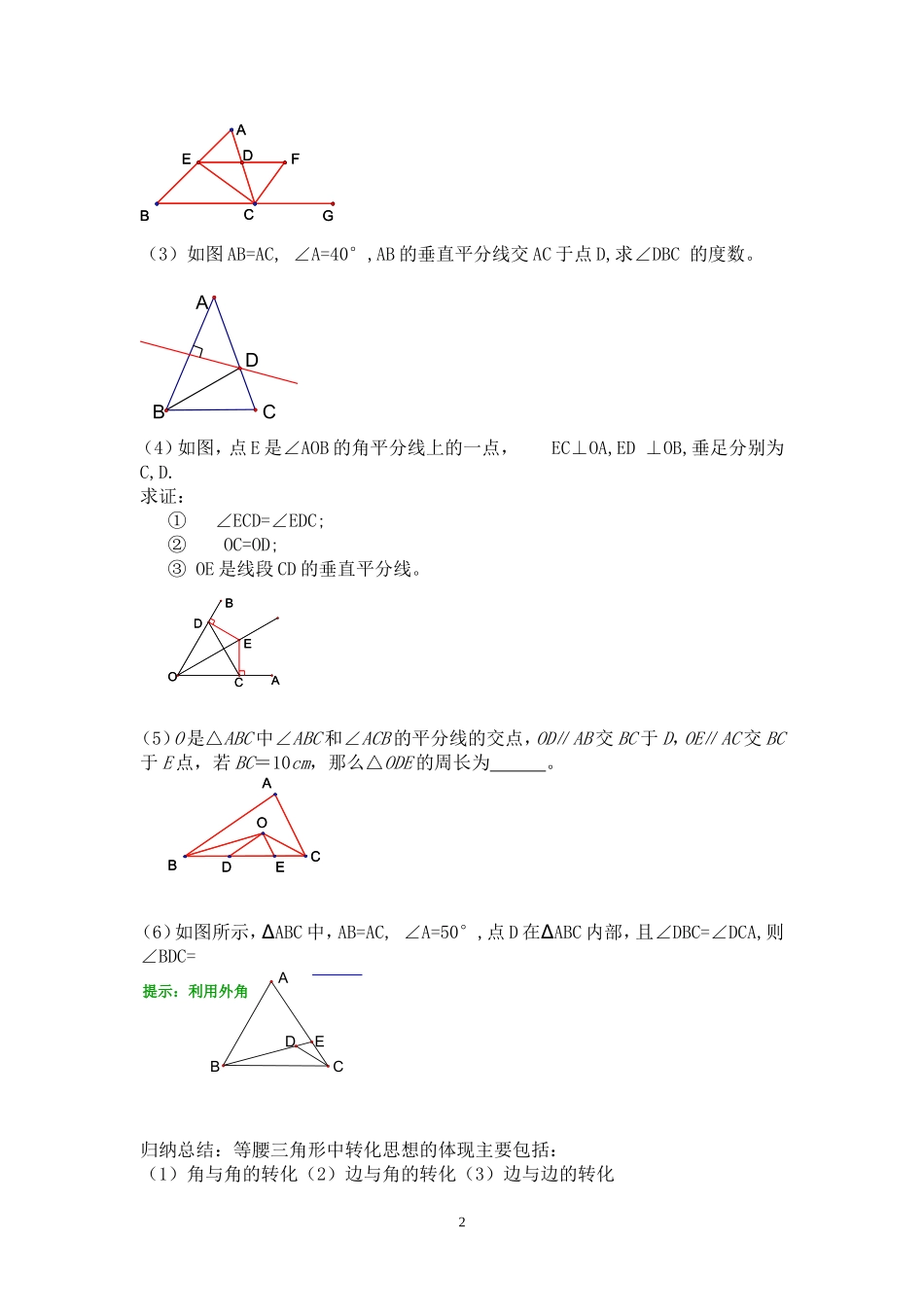
等腰三角形一、学习目标:1、能灵活应用等腰三角形的性质和识别条件解决有关问题2、在等腰三角形中腰与底边不明确或者顶角与底角不明确时,要体会分类讨论思想3、在解决有关问题时,体会角与角的转化、边与角的转化、边与边的转化的思想4、在解决有关角度问题时,常用设未知数列方程来解决,体会方程思想5、在评价的过程中,体会学习的乐趣二、学习过程:(一)、知识点回顾(请同学们完成如下填空,并试着用知识树的形式梳理一下本节的知识点,构建知识体系)1、等腰三角形的性质(1)有相等的三角形叫做等腰三角形。(2)等腰三角形的两个底角。(3)等腰三角形底边上的、底边上的、顶角的三线合一。(4)等腰三角形是图形,其对称轴是。2、等腰三角形的判定(1)有的三角形是等腰三角形(2)有的三角形是等腰三角形,简写成。(二)、分类思想的具体实践1、(请同学们完成下列填空题,认真体会每一道题中变式前、后的条件有什么不同,它对结果有怎样的影响?)(1)等腰三角形有两边长分别为3cm、4cm,则周长为cm。(2)等腰三角形有两边长分别为2cm、4cm,则周长为cm。(3)等腰三角形有一个内角为70°,则一个底角为度。(4)等腰三角形有一个内角为100°,则一个底角为度。2、归纳总结:等腰三角形中出现的分类讨论思想主要包括:角的分类讨论、边的分类讨论。总结一下:(1)角的问题在什么条件下需分类讨论?(2)边的问题在什么情况下需分类讨论?(三)、转化思想的具体实践(1)如图,∠A=∠B,CE∥DA,CE交AB于E,求证:∆CEB是等腰三角形DAEBC(2)如图,已知CE、CF分别平分∠ACB和它的外角,EF∥BC,EF交AC于D,你能说明DE=DF的理由吗?1FDEABCGFDEABCG(3)如图AB=AC,∠A=40°,AB的垂直平分线交AC于点D,求∠DBC的度数。ABCD(4)如图,点E是∠AOB的角平分线上的一点,EC⊥OA,ED⊥OB,垂足分别为C,D.求证:①∠ECD=∠EDC;②OC=OD;③OE是线段CD的垂直平分线。CDOABECDOABE(5)O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为。EDOABCEDOABC(6)如图所示,∆ABC中,AB=AC,∠A=50°,点D在∆ABC内部,且∠DBC=∠DCA,则∠BDC=CABED提示:利用外角归纳总结:等腰三角形中转化思想的体现主要包括:(1)角与角的转化(2)边与角的转化(3)边与边的转化2(四)、方程思想在等腰三角形中的运用如图,在△ABC中,AB=AC,过点B作∠ABC的平分线,交AC于D,当∠A是多少度时,ABCDE(五)、辅助线思想(1)已知:如图,AB=AC,DB=DC证明:∠C=∠BABCD2)已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,你能判断出BD与CE相等吗?请说出你判断的理由。FDECBA(六)、画图思想1、等腰三角形腰上的高与底边的夹角为α,则顶角β与α之间的关系是。2、一个等腰三角形顶角为钝角,则它的底角α的取值范围是。3、等腰三角形两底角平分线相等吗?两腰上的中线呢?两腰上的高呢?(七)、其它思想在等腰△ABC中,AB=AC,若过B、C两点分别作BE⊥AC于E,CF⊥AB于F,则BE=CF吗?请说明理由。FECBA3三、练习(1)判断下列语句是否正确。1、等腰三角形的角平分线、中线和高互相重合。()2、有一个角是60°的等腰三角形,其它两个内角也为60°.()3、等腰三角形的底角都是锐角.()4、钝角三角形不可能是等腰三角形.()2)如图,在等腰直角三角形ABC中,∠C=90°,AC=BC,AE平分∠BAC,ED⊥AB于点E。ABCDEABCDE1、若CE=2,则DE=____,DB=___2、你还能找出图中哪些相等的线段?3、若AB=8,则ΔDEB的周长为多少?(3)如图,AB=AC,D为AB上一点,E为AC延长线上一点,且BD=CE,DE交BC于G。求证:DG=EGFGCABED(4)在∆ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是___ABCD四、总结45