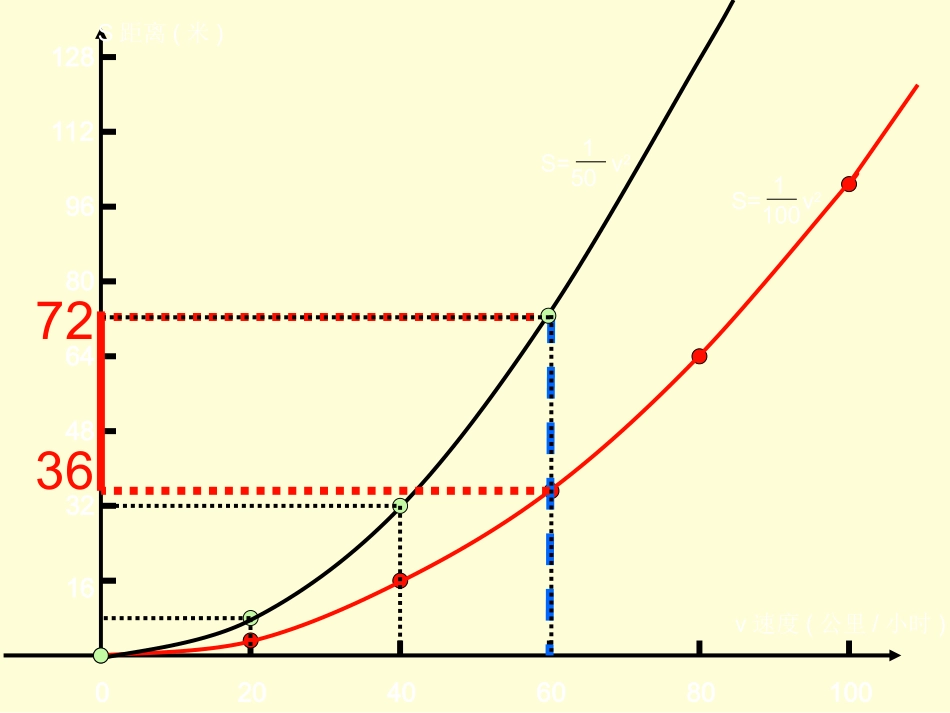
www.1230.org初中数学资源www.1230.org初中数学资源网网抛物线y=x2y=-x2开口方向增减性向上向下二次函数y=x2与y=-x2的性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值如图所示如图所示2xy2xy顶点坐标对称轴(0,0)即最低点(0,0)即最高点y轴(即直线x=0)最值当x=0时,最小值为0当x=0时,最大值为00204060801001632486480961121283672100S=1v250S=1v2v速度(公里/小时)S距离(米)xyoy=x2y=2x2-3-2-1123123456789xyo-3-2-123112-1-2-3-4-5-6-7y=-x2y=-2x2开口方向性质向上向下“左边”y随x的增大而减小顶点坐标对称轴(0,0)即最低点(0,0)即最高点y轴(直线x=0)最值当x=0时,y的最小值为0当x=0时,y的最大值为0y=ax2a>0a<0“右边”y随x的增大而增大y随x的增大而增大y随x的增大而减小张口大小由∣a∣的大小决定——∣a∣越大抛物线的张口越小y=x2y=2x2y=-x2y=-2x2xxyyOOwww.1230.org初中数学资源网1.2.3.-1-2-3.0.1.2.3.4.-1xy5y=2x2+1y=2x2www.1230.org初中数学资源网y=2x2+1y=2x20.xy0.xyy=-2x2-1y=-2x2二次函数y=ax2与y=ax2+c的图象有什么关系?二次函数y=ax2+c的图象可以由y=ax2的图象当c>0时向上平移c个单位得到.当c<0时向下平移-c个单位得到.函数关系式开口方向对称轴顶点坐标y=ax2y=ax2+ca>0向上;a<0向下y轴(直线x=0)(0,0)a>0向上;a<0向下(0,c)y轴(直线x=0)y=2x2+1y=2x20xyy=-2x2-1y=-2x20xy开口方向性质向上向下“左边”(x<0)y随x的增大而减小顶点坐标对称轴(0,c)即最低点(0,c)即最高点最值当x=0时,y的最小值为c当x=0时,y的最大值为cy=ax2+ca>0a<0y轴(直线x=0)“右边”(x>0)y随x的增大而增大y随x的增大而增大y随x的增大而减小开口大小由∣a∣的大小决定——∣a∣越大抛物线的开口越小1.函数y=x2-1的图象,可由y=x2的图象向___平移个单位.2.把函数y=3x2+2的图象沿x轴对折,得到的图象的函数解析式为.3.已知(m,n)在y=ax2+a的图象上,(-m,n)_____(在,不在)y=ax2+a的图象上.4.若y=x2+(2k-1)的顶点位于x轴上方,则K_______例题讲解下1y=-3x2-2在>0.5