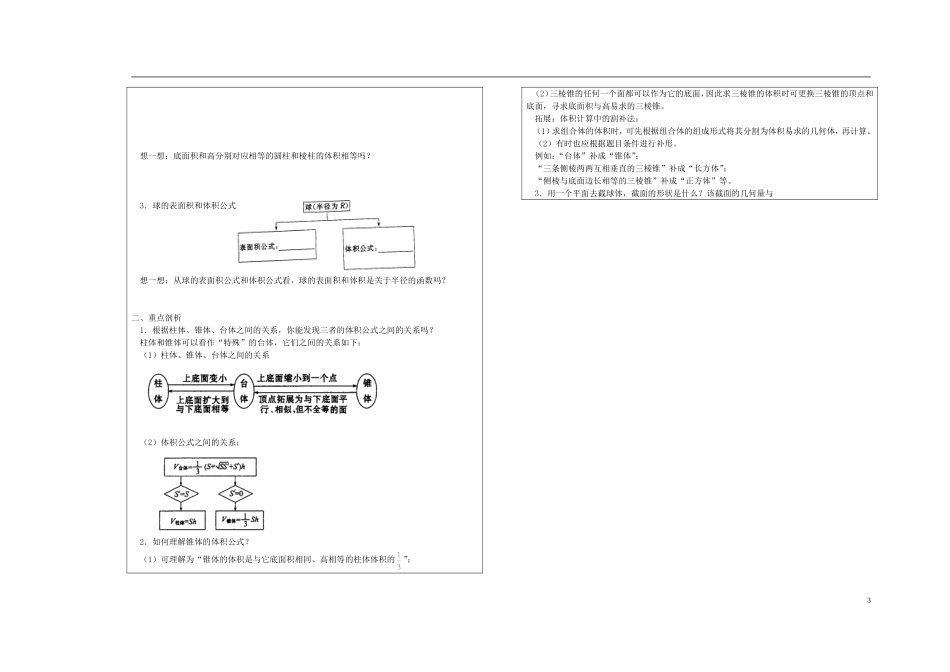
空间几何体的表面积和体积教学目标通过展开柱锥台的侧面,进一步认识柱锥台的表面积的计算公式。重点难点柱锥台的侧面积和表面积的求法。课堂结构一、自主探究1.几种特殊的多面体(1)直棱柱:侧棱和底面的棱柱叫做直棱柱。(2)正棱柱:底面为的直棱柱叫做正棱柱。(3)正棱锥:一个棱锥的底面是,并且顶点在底面的正投影是,称这样的棱锥为正棱锥,正棱锥的都相等。(4)正棱台:被平行于底面的平面所截,和之间的部分叫做正棱台。想一想:正方体、长方体是直棱柱吗?是正棱柱吗?底面是正多边形的棱锥是正棱锥吗?2.几种简单几何体的侧面展开图与侧面积想一想:正棱锥、正棱台中的斜高与侧棱相同吗?两者之间有何关系?二、重点剖析1.直棱柱和正棱柱各有什么特征,两者有何联系?(1)直棱柱和正棱柱均具有棱柱的所有性质,但直棱柱的侧面是矩形,正棱柱的侧面都是全等的矩形。(2)无论是直棱柱还是正棱柱,其侧棱均垂直于底面,即侧棱长即为棱柱的高。(3)由正棱柱的概念可知,正棱柱一定是直棱柱,但直棱柱不一定是正棱柱,因为直棱柱的底面不一定是正多边形。2.正棱柱、正棱锥、正棱台的侧面积之间的关系及求法是什么?(1)这三种几何体侧面积之间的关系(2)求这三种几何体侧面积的常见策略①正棱柱、正棱锥、正棱台的所有侧面都全等,因此求侧面积时,可先求一个侧面的面积,然后乘以侧面的个数。②棱台是由棱锥所截得到的,因此棱台的侧面积可由大小棱锥侧面积作差得到。拓展:正棱锥中几个重要的直角三角形(1)侧棱、高、底面正多边形外接圆的半径构成直角三角形;(2)侧棱、斜高、底面边长的一半构成直角三角形;(3)斜高、高、边心距离构成直角三角形。3.如何理解圆柱、圆锥、圆台的侧面积?(1)这三种几何体侧面积之间的关系(2)公式的记忆策略:重过程与原理,从其侧面展开图入手,利用平面几何中的面积计算公式推导侧面展开图的面积公式,并适当化简。(3)轴截面的作用旋转体中轴截面可以将母线、底面半径、高等主要元素联系在一起,因此处理好轴截面中的边角关系是正确计算的关键。三、例题讲解例1.如图所示,已知圆锥的底面半径为R,高为3R,(1)若它的内接圆柱的底面半径为,求该圆柱的表面积;(2)在它的所有内接圆柱中,表面积的最大值是多少?1[变式训练]:已知梯形ABCD中,AD//BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求旋转体的表面积。例2.正四棱锥的侧面积是底面积的2倍,高是3,求它的表面积。[变式训练]:已知一正三棱台的两底面边长分别为30cm和20cm,且其侧面积等于两底面积之和,求棱台的高。例3.如图是一建筑物的三视图(单位:m),现需将其外壁用油漆粉刷一遍,已知每平方米用漆0.2kg,问需要油漆多少千克?(无需求近似值)[变式训练]:如图是一个烟筒的直观图(图中单位:cm),它的下部是一个四棱台(上、下底面均是正方形,侧面是全等的等腰梯形)形物体;上部是一个四棱柱(底面与四棱台的上底面重合,侧面是全等的矩形)形物体,为防止雨水的侵蚀,增加美观,需要粘贴瓷砖,需要瓷砖多少平方厘米(无需求近似值)。四、归纳小结1.旋转体的轴截面是化空间问题为平面问题的重要工具,因为在轴截面中集中体现了旋转体的“关键量”之间的关系,在推导这些量之间的关系时要注意比例性质的应用。2.棱锥、棱台的表面积为其侧面积与底面积之和,底面积据平面几何知识求解,侧面积关键是求斜高和底面边长。斜高、侧棱及其在底面的射影与高、底面边长这四条线段可以构成直角三角形(或梯形),因此利用好这些直角三角形(或梯形)是解题的关键。3.三视图与求空间几何体的表面积问题结合是常见的例题形式,此类问题要先从几何体三视图特征反推得到实物组合体的形状及相关数量,然后直接应用圆锥与正四棱柱的表面积或侧面积公式运算。学后、教后反思:高二年级数学教学案(2010年9月29日)周次5课题空间几何体的体积2课时授课形式新授主编审核教学目标1.求空间几何体的体积。2.常与函数、三视图、线面位置关系等知识相结合求最值。3.球与正方体等简单几何...