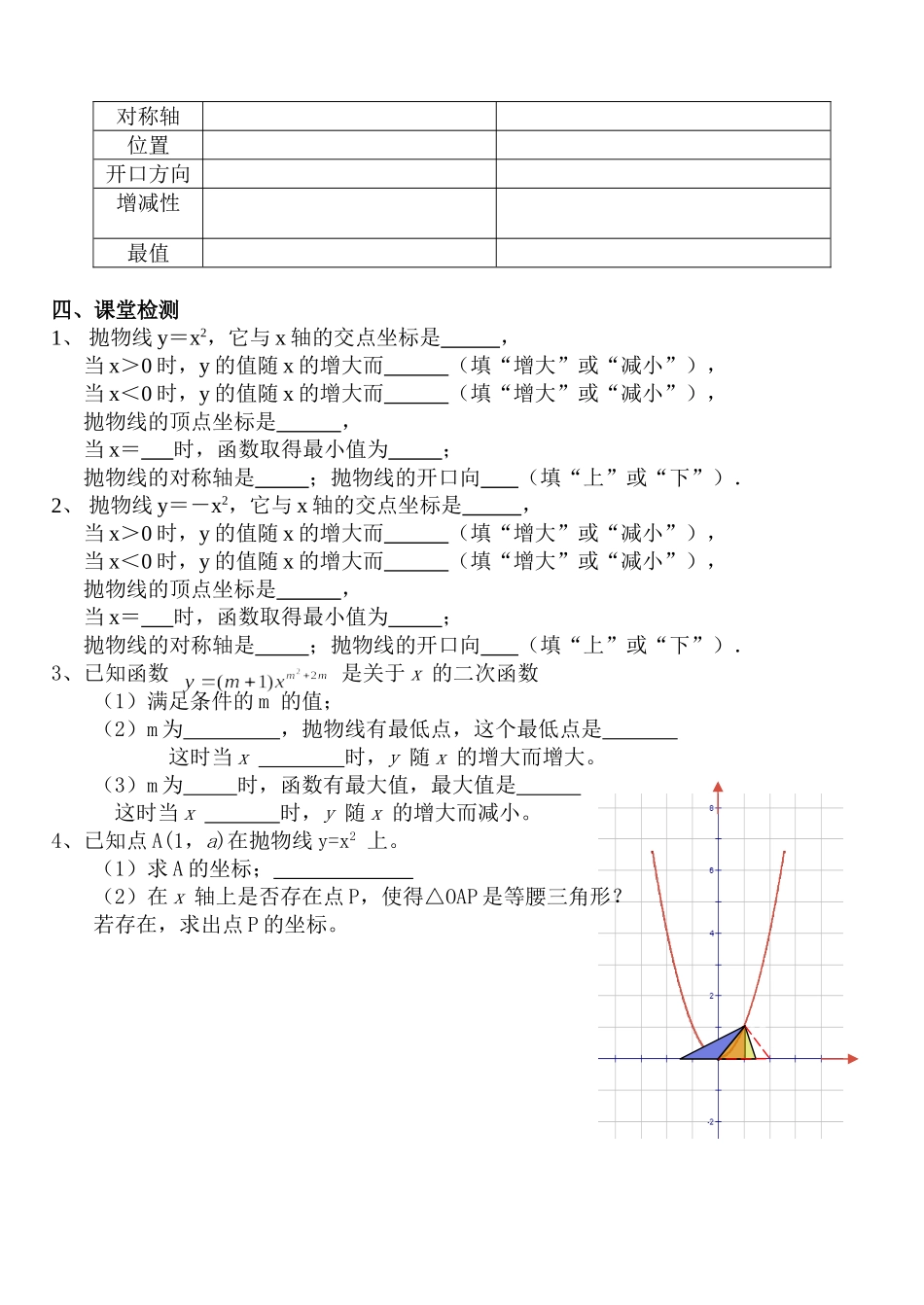
2.2结识抛物线导学案一、学习目标1.能够作出函数y=x2的图象,通过对图像的观察得出二次函数性质。2.猜想并能作出y=-x2的图象,能比较它与y=x2的图象的异同.二、学习过程回顾思考:(1)一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数叫做x的___________.(2)画函数的图象的主要步骤:、、。新知探究:活动一:1、作出函数y=x2的图像并回答下列问题:(1)选择适当的x的值,并计算相应的y的值完成下表XY(2)在直角坐标系中描点(3)用光滑的曲线连接各点,便得到y=x2的图像2、根据所作图像回答下列问题:(1)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点.(2)图象与x轴有交点吗?如果有,交点坐标是什么?(3)当x<0时,随着x的值增大,y的值当x>0时随着x的值增大,y的值(4)当x取,y的值最小;最小值是总结:y=x的图象的性质:二次函数y=x的图像是一条线,它的开口向,且关于对称。对称轴与抛物线的交点是抛物线的,它是图像的。活动二:1、类比y=x2探究y=-x2的图像性质,先想一想,然后作出它的图象(作在课本上)函数y=-x2的图象形状是,它与二次函数y=x2的图象关系是2、y=-x的图象的性质:(1)图象与x轴交于(2)y0(3)当x<0时,y随x的增大而,当x>0时,y随x的增而。(4)y的最大值是,此时x的值为。(5)图象关于对称三、课堂小结二次函数y=±x2的性质,根据图形填表抛物线y=x2y=-x2顶点坐标oyxA对称轴位置开口方向增减性最值四、课堂检测1、抛物线y=x2,它与x轴的交点坐标是,当x>0时,y的值随x的增大而(填“增大”或“减小”),当x<0时,y的值随x的增大而(填“增大”或“减小”),抛物线的顶点坐标是,当x=时,函数取得最小值为;抛物线的对称轴是;抛物线的开口向(填“上”或“下”).2、抛物线y=-x2,它与x轴的交点坐标是,当x>0时,y的值随x的增大而(填“增大”或“减小”),当x<0时,y的值随x的增大而(填“增大”或“减小”),抛物线的顶点坐标是,当x=时,函数取得最小值为;抛物线的对称轴是;抛物线的开口向(填“上”或“下”).3、已知函数是关于x的二次函数(1)满足条件的m的值;(2)m为,抛物线有最低点,这个最低点是这时当x时,y随x的增大而增大。(3)m为时,函数有最大值,最大值是这时当x时,y随x的增大而减小。4、已知点A(1,a)在抛物线y=x2上。(1)求A的坐标;(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标。