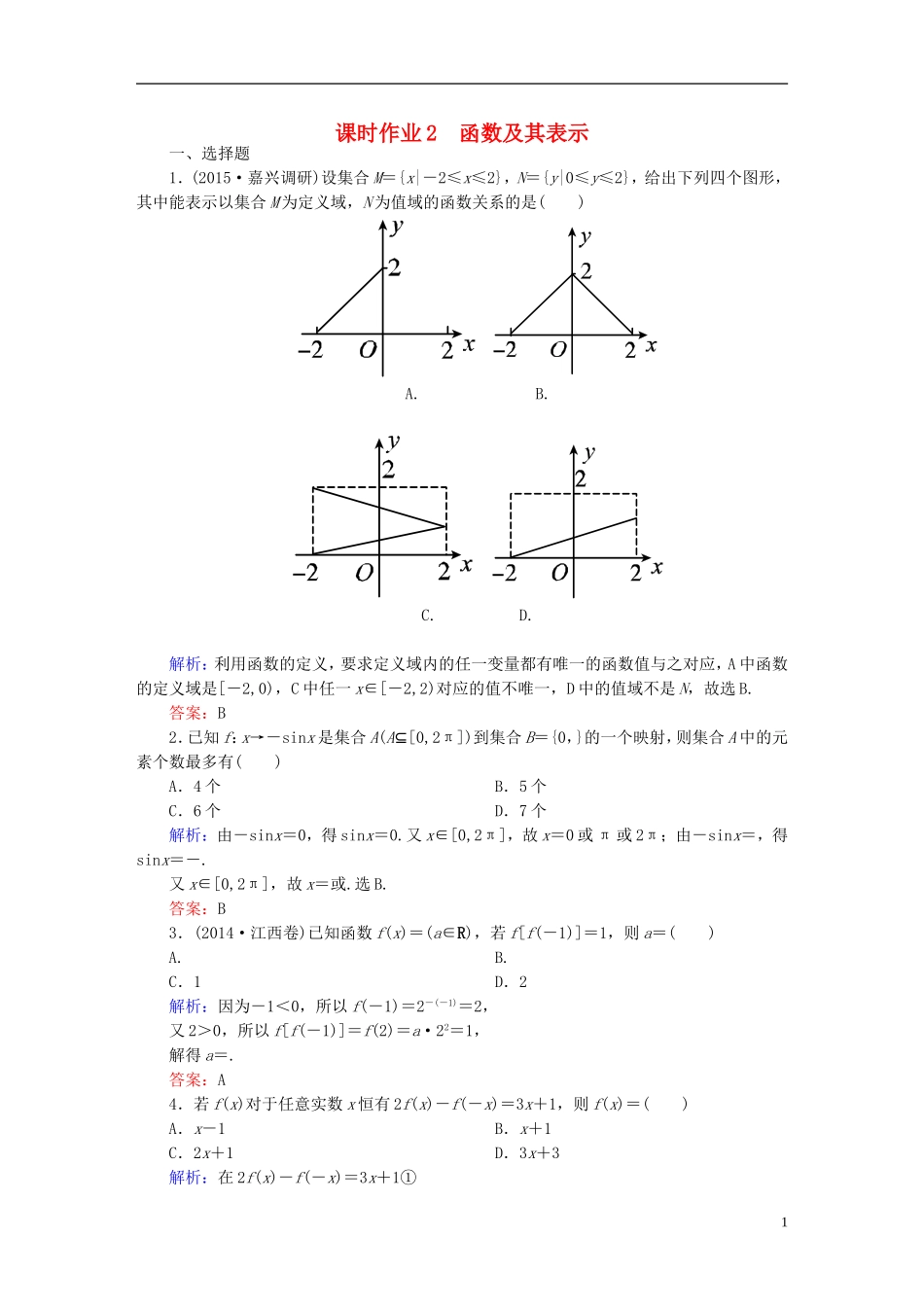
课时作业2函数及其表示一、选择题1.(2015·嘉兴调研)设集合M={x|-2≤x≤2},N={y|0≤y≤2},给出下列四个图形,其中能表示以集合M为定义域,N为值域的函数关系的是()A.B.C.D.解析:利用函数的定义,要求定义域内的任一变量都有唯一的函数值与之对应,A中函数的定义域是[-2,0),C中任一x∈[-2,2)对应的值不唯一,D中的值域不是N,故选B.答案:B2.已知f:x→-sinx是集合A(A⊆[0,2π])到集合B={0,}的一个映射,则集合A中的元素个数最多有()A.4个B.5个C.6个D.7个解析:由-sinx=0,得sinx=0.又x∈[0,2π],故x=0或π或2π;由-sinx=,得sinx=-.又x∈[0,2π],故x=或.选B.答案:B3.(2014·江西卷)已知函数f(x)=(a∈R),若f[f(-1)]=1,则a=()A.B.C.1D.2解析:因为-1<0,所以f(-1)=2-(-1)=2,又2>0,所以f[f(-1)]=f(2)=a·22=1,解得a=.答案:A4.若f(x)对于任意实数x恒有2f(x)-f(-x)=3x+1,则f(x)=()A.x-1B.x+1C.2x+1D.3x+3解析:在2f(x)-f(-x)=3x+1①1将①中x换为-x,则有2f(-x)-f(x)=-3x+1②①×2+②得3f(x)=3x+3,∴f(x)=x+1.答案:B5.图中的图象所表示的函数的解析式为()A.y=|x-1|(0≤x≤2)B.y=-|x-1|(0≤x≤2)C.y=-|x-1|(0≤x≤2)D.y=1-|x-1|(0≤x≤2)解析:取x=1,则y=,只有B、C满足.取x=0,则y=0,在B、C中只有B满足,所以选B.答案:B6.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为()A.y=[]B.y=[]C.y=[]D.y=[]解析:当各班人数除以10的余数大于6时再增选一名代表,可以看作先用该班人数除以10再用这个余数与3相加,若和大于等于10就增选一名代表,将二者合并便得到推选代表人数y与该班人数x之间的函数关系,用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为y=[].答案:B二、填空题7.已知f=x2+,则函数f(3)=________.解析:∵f=x2+=2+2,∴f(x)=x2+2,∴f(3)=32+2=11.答案:118.(2014·浙江卷)设函数f(x)=若f(f(a))=2,则a=__________.解析:当a≤0时,f(a)=a2+2a+2>0,f(f(a))<0,显然不成立;当a>0时,f(a)=-a2,f(f(a))=a4-2a2+2=2,则a=±或a=0,故a=.答案:9.(2014·新课标全国卷Ⅰ)设函数f(x)=则使得f(x)≤2成立的x的取值范围是__________.解析:当x<1时,由ex-1≤2得x≤1+ln2,∴x<1;当x≥1时,由x≤2得x≤8,∴1≤x≤8.综上,符合题意的x的取值范围是x≤8.答案:(-∞,8]三、解答题210.二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.(1)求f(x)的解析式;(2)解不等式f(x)>2x+5.解析:(1)设二次函数f(x)=ax2+bx+c(a≠0).∵f(0)=1,∴c=1.把f(x)的表达式代入f(x+1)-f(x)=2x,有a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.∴2ax+a+b=2x.∴a=1,b=-1.∴f(x)=x2-x+1.(2)由x2-x+1>2x+5,即x2-3x-4>0,解得x>4或x<-1.故原不等式解集为{x|x>4或x<-1}.11.函数f(x)对一切函数x、y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,(1)求f(0)的值;(2)试确定函数f(x)的解析式.解析:(1)令x=1,y=0,得f(1)-f(0)=2.又∵f(1)=0,∴f(0)=-2.(2)令y=0,则f(x)-f(0)=x(x+1),由(1)知,f(x)=x(x+1)+f(0)=x(x+1)-2=x2+x-2.12.已知函数f(x)=满足f(c2)=.(1)求常数c的值;(2)解不等式f(x)>+1.解析:(1)因为0<c<1,所以c2<c,由f(c2)=,即c3+1=,c=.(2)由(1)得f(x)=由f(x)>+1得,当0<x<时,解得<x<,当≤x<1时,解得≤x<,所以f(x)>+1的解集为{x|<x<}.3