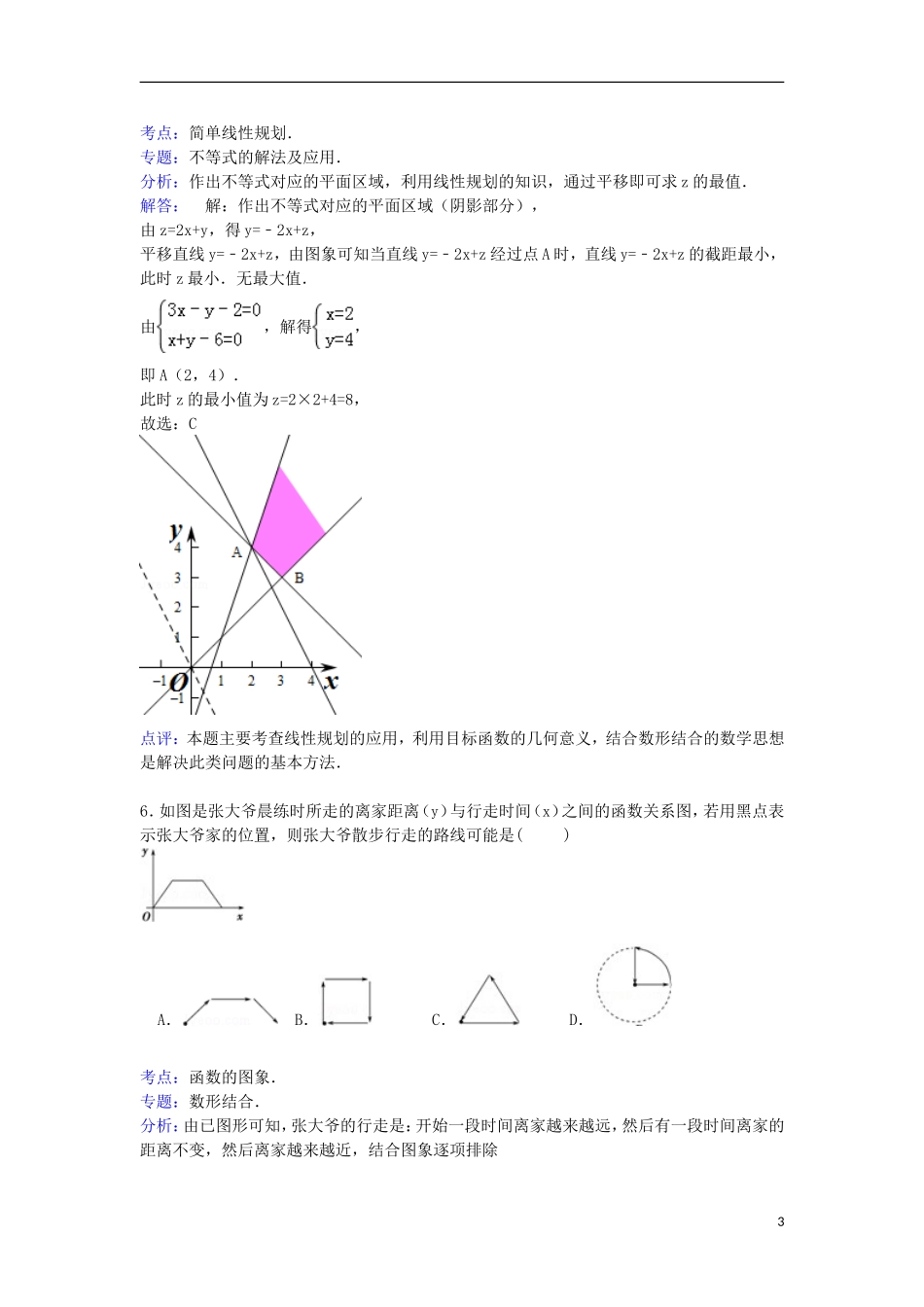
湖北省七市(州)联考2015届高考数学模拟试卷(文科)(4月份)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数z满足z(1﹣i)=2(i是虚数单位),则z=()A.1+iB.﹣1+iC.﹣1﹣iD.1﹣i考点:复数代数形式的乘除运算.专题:数系的扩充和复数.分析:利用复数的运算法则、共轭复数的定义即可得出.解答:解: z(1﹣i)=2,∴z(1﹣i)(1+i)=2(1+i),∴z=1+i.故选:A.点评:本题考查了复数的运算法则、共轭复数的定义,属于基础题.2.若命题p为真命题,命题q为假命题,则以下为真命题的是()A.p∧qB.p∧(¬q)C.(¬p)∨qD.(¬p)∧(¬q)考点:复合命题的真假.专题:简易逻辑.分析:命题p为真命题,命题q为假命题,可得¬q为真命题,再利用复合命题真假的判定方法即可得出.解答:解: 命题p为真命题,命题q为假命题,∴¬q为真命题,∴p∧(¬q)为真命题,故选:B.点评:本题考查了复合命题真假的判定方法,属于基础题.3.集合M={x|x=sinθ,θ∈R},N={x|≤2x≤8},则M∩N=()A.B.[﹣1,3]C.D.考点:交集及其运算.专题:集合.分析:利用正弦函数的值域求出x的范围确定出M,求出N中不等式的解集确定出N,找出两集合的交集即可.解答:解:由M中x=sinθ,θ∈R,得到﹣1≤x≤1,即M=[﹣1,1],由N中不等式变形得:=≤2x≤8=23,即≤x≤3,∴N=[,3],1则M∩N=[,1],故选:D.点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.4.如图,分别以正方形ABCD的四条边为直径画半圆,重叠部分如图中阴影区域,若向该正方形内随机投一点,则该点落在阴影区域的概率为()A.B.C.D.考点:几何概型.专题:概率与统计.分析:由题意知本题是一个几何概型,试验发生包含的所有事件是矩形面积,而满足条件的阴影区域,可以通过空白区域面得到,空白区域可以看作是由8部分组成,每一部分是由边长为的正方形面积减去半径为的四分之一圆的面积得到.解答:解:如图,由题意知本题是一个几何概型,设正方形ABCD的边长为2, 试验发生包含的所有事件是矩形面积S=2×2=4,空白区域的面积是2(4﹣π)=8﹣2π,∴阴影区域的面积为4﹣(8﹣2π)=2π﹣4∴由几何概型公式得到P==﹣1,故选B.点评:本题考查几何概型、等可能事件的概率,且把几何概型同几何图形的面积结合起来,几何概型和古典概型是高中必修中学习的,2015届高考时常以选择和填空出现,有时文科会考这种类型的解答.5.已知变量x,y满足条件,则目标函数z=2x+y()A.有最小值3,最大值9B.有最小值9,无最大值C.有最小值8,无最大值D.有最小值3,最大值82考点:简单线性规划.专题:不等式的解法及应用.分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最值.解答:解:作出不等式对应的平面区域(阴影部分),由z=2x+y,得y=﹣2x+z,平移直线y=﹣2x+z,由图象可知当直线y=﹣2x+z经过点A时,直线y=﹣2x+z的截距最小,此时z最小.无最大值.由,解得,即A(2,4).此时z的最小值为z=2×2+4=8,故选:C点评:本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.6.如图是张大爷晨练时所走的离家距离(y)与行走时间(x)之间的函数关系图,若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是()A.B.C.D.考点:函数的图象.专题:数形结合.分析:由已图形可知,张大爷的行走是:开始一段时间离家越来越远,然后有一段时间离家的距离不变,然后离家越来越近,结合图象逐项排除3解答:解:由已图形可知,张大爷的行走是:开始一段时间离家越来越远,然后有一段时间离家的距离不变,然后离家越来越近,C符合;A:行走路线是离家越来越远,不符合;B:行走路线没有一段时间离家的距离不变,不符;C:行走路线没有一段时间离家的距离不变,不符;故选:D点评:本题主要考查了识别图象的及利用图象解决实际问题的能力,还要注意排除法在解题中的应用.7.已知点A(﹣1,0),B(1,0),过定点M(0,2)的直线l上存在点P,使得,则直线...