正弦函数、余弦函数的图象和性质1VIP免费

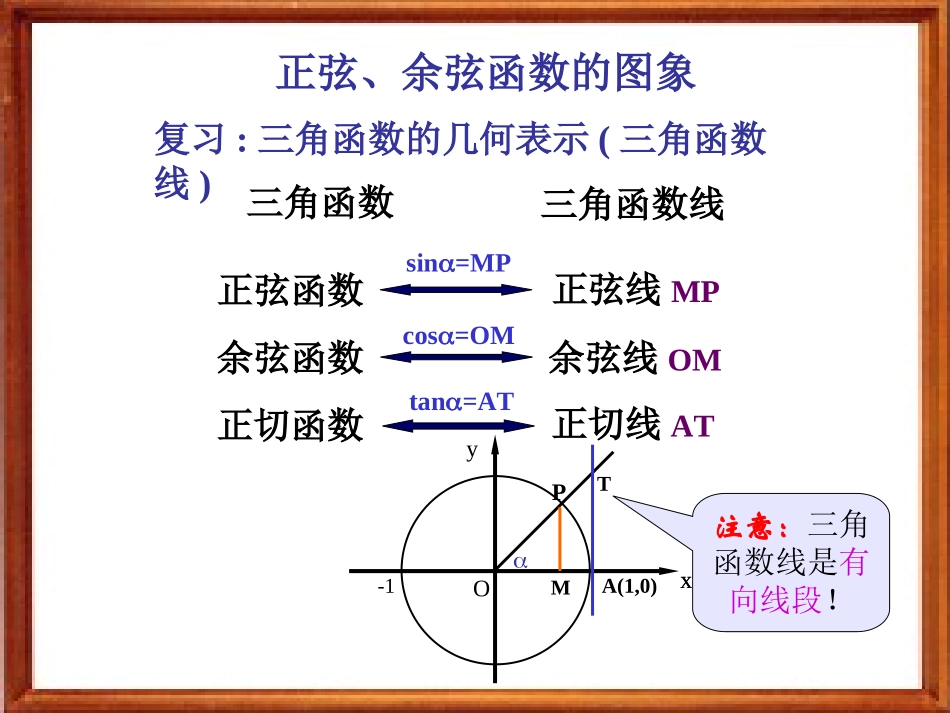
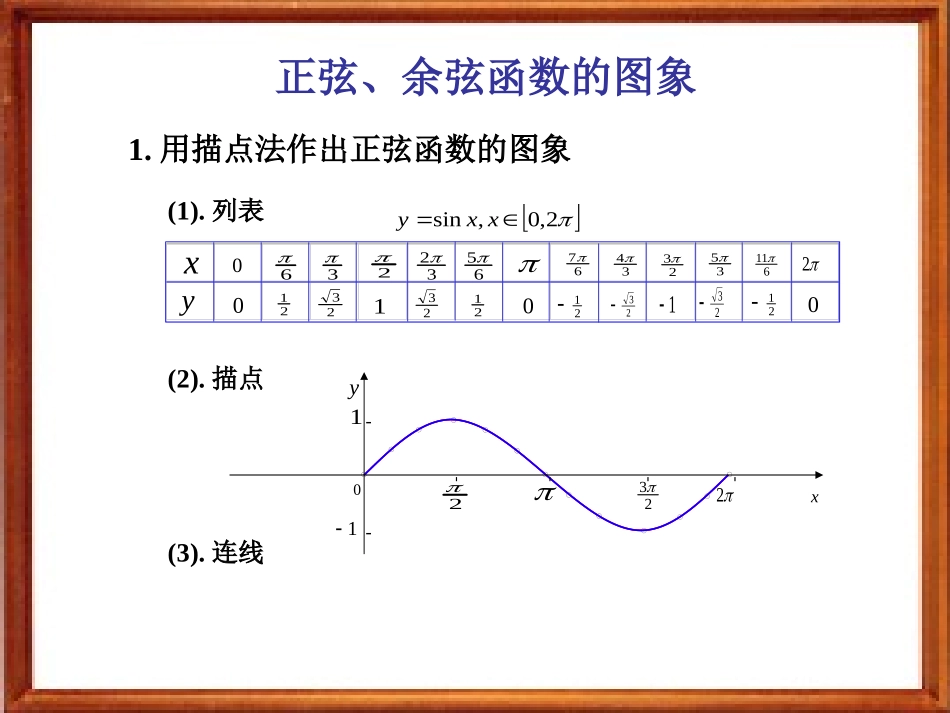
正弦、余弦函数的图象X三角函数三角函数线正弦函数余弦函数正切函数正弦线MP复习:三角函数的几何表示(三角函数线)yxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！余弦线OM正切线AT正弦、余弦函数的图象(1).列表(2).描点(3).连线632326567342335611202123012123212300212312,0,sinxxy1.用描点法作出正弦函数的图象---223xy0211---xy正弦、余弦函数的图象O1Oyx33234352-11连线：用光滑曲线将这些正弦线的终点连结起来AB2.用三角函数线作出正弦函数的图象几何法作图的关键是如何利用单位圆中角x的正弦线，巧妙地移动到直角坐标系内，从而确定对应的点1(x,sinx).正弦、余弦函数的图象x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxRyxo1-122322正弦曲线因为终边相同的角的三角函数值相同，所以y=sinx的图象在……，……与y=sinx,x[0,2π]∈的图象相同2,4,0,2,,2,0,4,2正弦、余弦函数的图象yxo1-122322如何在精确度要求不太高时作出正弦函数的图象?(0,0)(,1)2(,0)(,-1)23(2,0)五点画图法五点法——(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)(0,0)(,1)2(,0)(,-1)23(2,0)xsinx22302010-10正弦、余弦函数的图象x6yo--12345-2-3-41正弦、余弦函数的图象余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同正弦、余弦函数的图象例1画出函数y=1+sinx，x[0,2]的简图：xsinx1+sinx22302010-1012101o1yx22322-12y=sinx，x[0,2]y=1+sinx，x[0,2]步骤：1.列表2.描点3.连线正弦、余弦函数的图象例2画出函数y=-cosx，x[0,2]的简图：xcosx-cosx2230210-101-1010-1yxo1-122322y=-cosx，x[0,2]y=cosx，x[0,2]正弦、余弦函数的图象xsinx2230210-101练习：在同一坐标系内，用五点法分别画出函数y=sinx，x[0,2]和y=cosx，x[,]的简图：223o1yx22322-12y=sinx，x[0,2]y=cosx，x[,]223向左平移个单位长度2xcosx100-1022302正弦、余弦函数的图象小结1.正弦曲线、余弦曲线的联系和区别2.五点作图法：与x轴的交点，最高点，最低点，即x取yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]2,23,,2,0作业：P64习题4.8第1题谢谢大家