中考数学压轴题分析张VIP免费

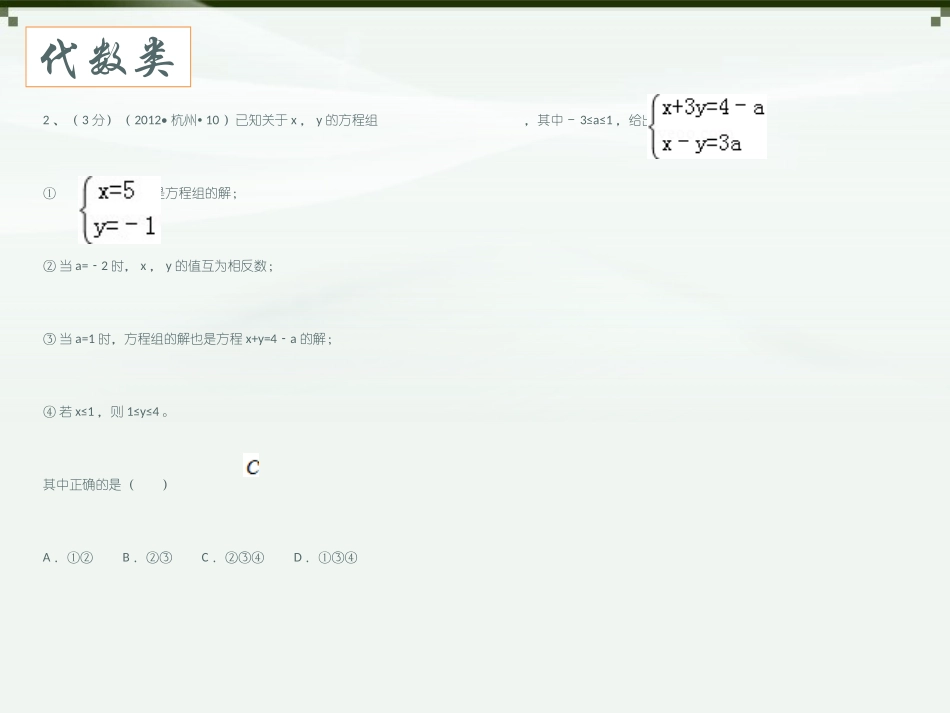
近三年中考数学压轴题分析代数类1、（3分）（2013•杭州•10）给出下列命题及函数y=x，y=x2和y=①如果，那么0＜a＜1；②如果，那么a＞1；③如果，那么﹣1＜a＜0；④如果，那么a＜﹣1。则（）A.正确的命题是①④B.错误的命题是②③④C.正确的命题是①②D.错误的命题只有③2、（3分）（2012•杭州•10）已知关于x，y的方程组，其中﹣3≤a≤1，给出下列结论：①是方程组的解；②当a=2﹣时，x，y的值互为相反数；③当a=1时，方程组的解也是方程x+y=4a﹣的解；④若x≤1，则1≤y≤4。其中正确的是（）A．①②B．②③C．②③④D．①③④代数类代数类3、（3分）（2010•杭州•10）定义[]为函数的特征数,下面给出特征数为[2m，1–m,–1–m]的函数的一些结论：①当m=–3时，函数图象的顶点坐标是(，)；②当m>0时，函数图象截x轴所得的线段长度大于；③当m<0时，函数在x>时，y随x的增大而减小；④当m0时，函数图象经过同一个点。其中正确的结论有（）A.①②③④B.①②④C.①③④D.②④,,abc2yaxbxc31382341代数类4、（12分）（2012•杭州•22）在平面直角坐标系内，反比例函数和二次函数的图象交于点A（1，k）和点B（﹣1，﹣k）．（1）当k=﹣2时，求反比例函数的解析式；（2）要使反比例函数和二次函数都是y随着x的增大而增大，求k应满足的条件以及x的取值范围；（3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值。)1(2xxky代数类5、（10分）（2011•杭州•23）设函数（k为实数）（1）写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中，用描点法画出这两个特殊函数的图象；（2）根据所画图象，猜想出：对任意实数k，函数的图象都具有的特征，并给予证明；（3）对任意负实数k，当x＜m时，y随着x的增大而增大，试求出m的一个值。1)12(2xkkxy代数类6、（12分）（2014•杭州•23）复习课中，教师给出关于x的函数（k是实数）．教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上．学生思考后，黑板上出现了一些结论．教师作为活动一员，又补充一些结论，并从中选出以下四条：①存在函数，其图象经过（1，0）点；②函数图象与坐标轴总有三个不同的交点；③当x＞1时，不是y随x的增大而增大就是y随x的增大而减小；④若函数有最大值，则最大值比为正数，若函数有最小值，则最小值比为负数．教师：请你分别判断四条结论的真假，并给出理由．最后简单写出解决问题时所用的数学方法。1)14(22kxkkxy几何类：圆1、（4分）（2013•杭州•16）射线QN与等边△ABC的两边AB，BC分别交于点M，N，且AC∥QN，AM=MB=2cm，QM=4cm．动点P从点Q出发，沿射线QN以每秒1cm的速度向右移动，经过t秒，以点P为圆心，cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值（单位：秒）。几何类：圆2、（4分）（2010•杭州•16）如图,已知的中点，⊙O与AC，BC分别相切于点D与点E．点F是⊙O与AB的一个交点，连DF并延长交的延长线于点G.则CG=。ABOCBCACABC是.90,6,0几何类：圆3、（12分）（2012•杭州•23）如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OBAT⊥于点B，已知∠EAT=30°，AE=，MN=．（1）求∠COB的度数；（2）求⊙O的半径R；（3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比。33222几何类：三角形1、（3分）（2014•杭州•10）已知ADBC∥，ABAD⊥，点E，点F分别在射线AD，射线BC上．若点E与点B关于AC对称，点E与点F关于BD对称，AC与BD相交于点G，则（）A.B.C.D.2tan1ADBCFBC52DEFAEB0226cos4AGB几何类：三角形2、（4分）（2014•杭州•16）点A，B，C都在半径为r的圆上，直线AD⊥直线BC，垂足为D，直线BE⊥直线AC，垂足为E，直线AD与BE相交于点H．若BH=AC，则∠ABC所对的弧长等于（长度单位）。rr3531或几何类：三角形3、（4分）（2011•杭...