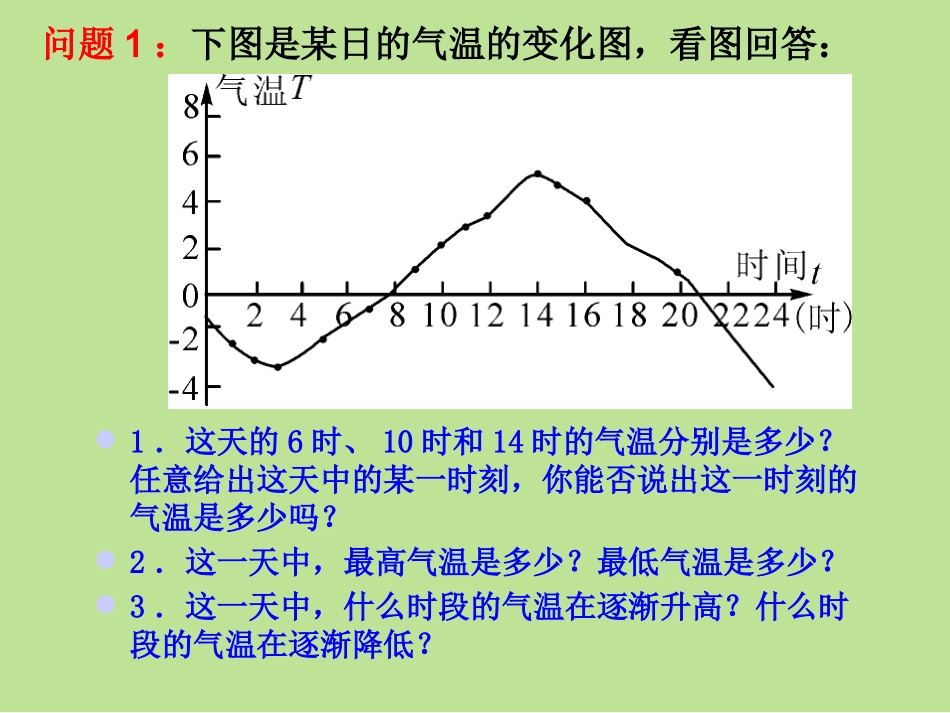
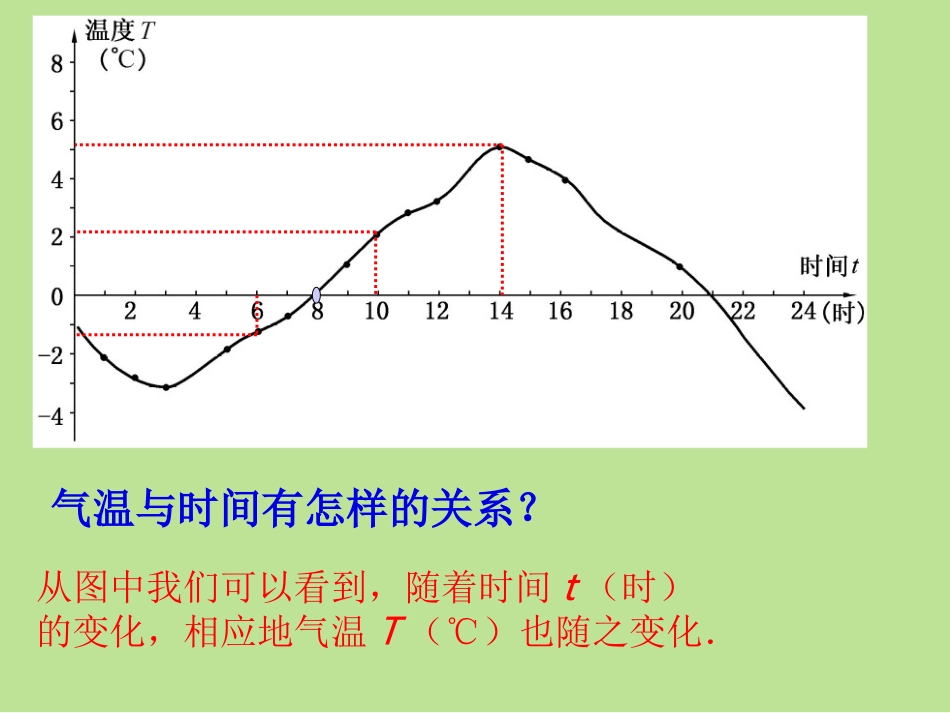
第17章函数及其图象17.1变量与函数第1课时变量与函数八年级下册问题1:下图是某日的气温的变化图,看图回答:1.这天的6时、10时和14时的气温分别是多少?任意给出这天中的某一时刻,你能否说出这一时刻的气温是多少吗?2.这一天中,最高气温是多少?最低气温是多少?3.这一天中,什么时段的气温在逐渐升高?什么时段的气温在逐渐降低?从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.气温与时间有怎样的关系?问题3收音机上的刻度盘的波长和频率分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数值:新课推进新课推进波长λ(m)30050060010001500频率f(kHz)1000600500300200同学们是否能从表格中找出波长λ与频率f的关系呢?λ·f=30000问题4:圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积,则S与r之间满足下列关系:S=____.利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:由此可以看出,圆的半径越大,它的面积就______.半径r(cm)11.522.63.2…圆面积S(cm2)…πr2π2.25π4π6.76π10.24π越大【归纳结论】在某一变化过程中,可以取不同数值的量,叫做变量.上面各个问题中,都出现了两个变量,它们互相依赖,密切相关.一般地,如果在一个变化过程中,有两个变量,例如x和y,对于x的每一个值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.表示函数关系的方法通常有三种:(1)解析法,如问题3中的f=300000/λ,问题4中的S=πr2,这些表达式称为函数的关系式.(2)列表法,如问题2中的小蕾的体重表,问题3中的波长与频率关系表.(3)图象法,如问题1中的气温曲线.在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量(constant),如问题3中的300000,问题4中的π等.运用新知运用新知1.常量和变量在研究“某一变化过程中”时是确定的,以s=vt为例(t为时间,v为速度,s为路程):①若速度v固定,则常量是_______,变量是_______;②若时间t固定,则常量是_______,变量是_______.分析:①速度v固定,即在这个变化过程中v的取值保持不变,此时s随t的变化而变化,可以取不同的数值,故v为常量,s和t为变量;②t固定,即为常量,此时s和v可以取不同的数值,是变量.解:①v,s、t;②t,s、v2.已知变量x与y的四种关系:y=︱x︱,︱y︱=x,2x2-y=0,2x-y2=0其中y是x的函数的有_____个.分析:依函数定义,︱y︱=x与2x-y2=0中,x每取一个大于0的值,y都有两个与之对应,例如x=4时,︱y︱=4,有y=±4,故y不是x的函数;只有y=︱x︱和2x2-y=0中y是x的函数.解:23.若一辆汽车以50千米/时的速度匀速行驶,则行驶的路程s(千米)与行驶的时间t(时)之间的函数关系式是()A.s=50+50tB.s=50tC.s=50-50tD.以上都不对B4.下列变量间的关系不是函数关系的是()A.长方形的宽一定,其长与面积B.正方形的周长与面积C.圆的半径与面积D.等腰三角形的底边长与面积D5.下列说法不正确的是()A.公式V=4/3πr3中,4/3是常量,r是变量,V是πr的函数B.公式V=4/3πr3中,V是r的函数C.公式v=s/t中,v可以是变量,也可以是常量D.圆的面积S是半径r的函数A填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么?图17.1.2如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.解如图能发现涂黑的格子成一条直线.函数关系式:y=10-x例1试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式.xy解:y与x的函数关系式:y=180-2x.如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分面积ycm2与MA长度xcm之间的函数关系式.图17.1.3解y与x的函数关系式:221xy.例2探索1在上面问题中所出现的各个函数中,自变量的取值有限制吗?如果有,写出它的取值范围.y=10-xy=180-2x221xyxy图17.1.3在用解析式表示函数时,要考虑自变量的取值必须使解析式有意义.如果遇到实际...