立体几何(8)VIP免费

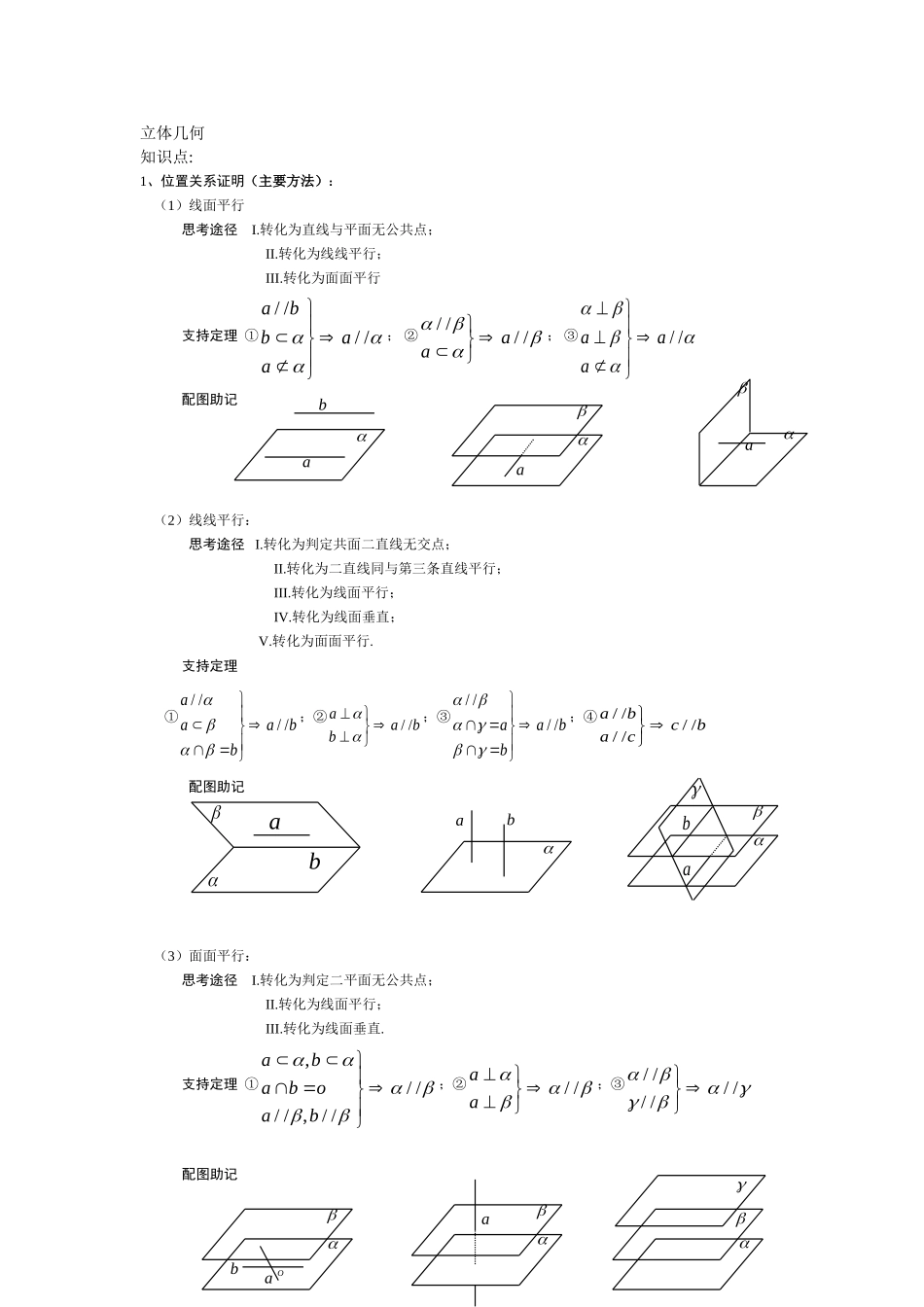
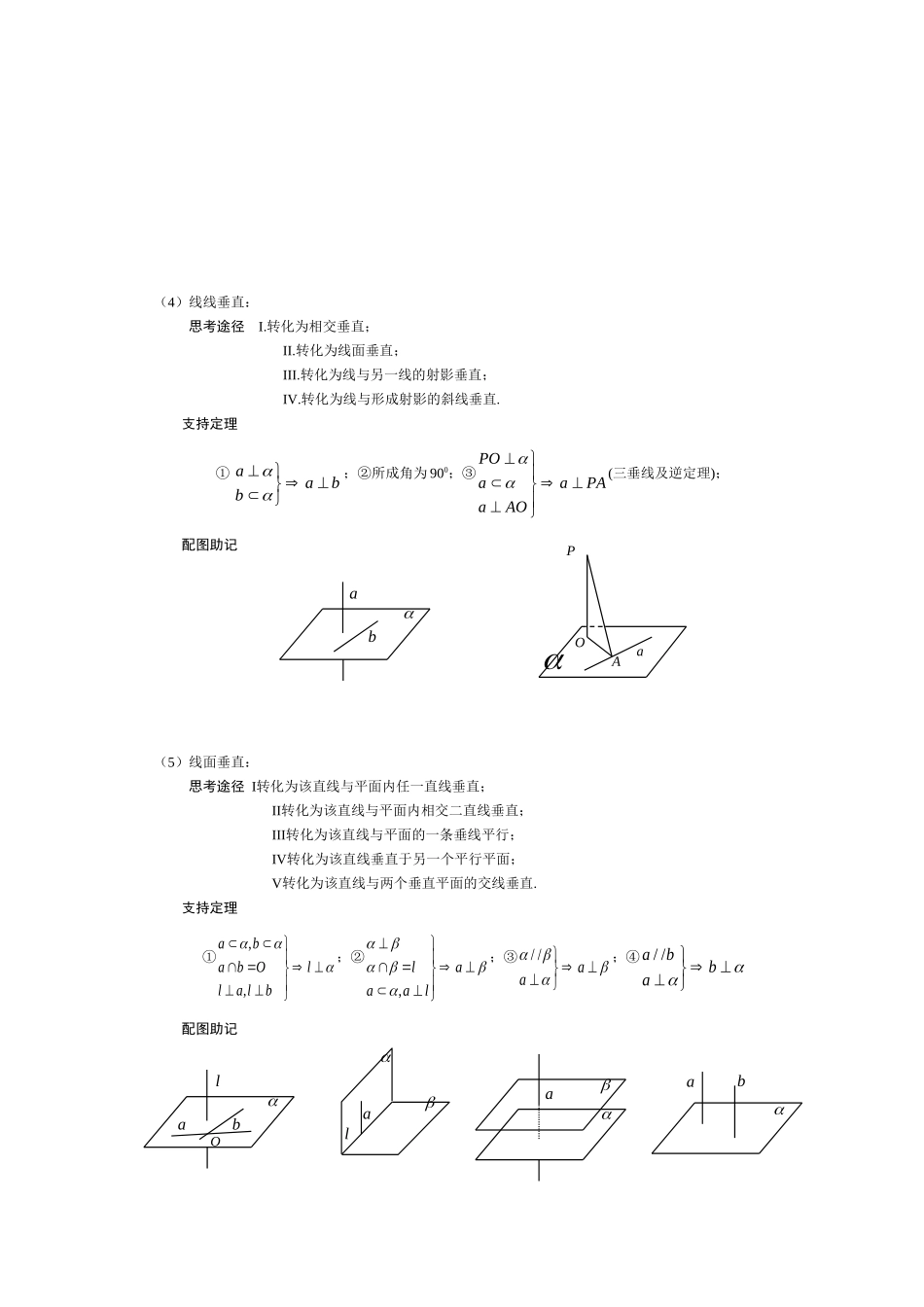
立体几何知识点:1、位置关系证明（主要方法）：（1）线面平行思考途径I.转化为直线与平面无公共点；II.转化为线线平行；III.转化为面面平行支持定理①////abbaa；②////aa；③//aaa配图助记（2）线线平行：思考途径I.转化为判定共面二直线无交点；II.转化为二直线同与第三条直线平行；III.转化为线面平行；IV.转化为线面垂直；V.转化为面面平行.支持定理①////aaabb；②//aabb；③////aabb；④//////abcbac配图助记（3）面面平行：思考途径I.转化为判定二平面无公共点；II.转化为线面平行；III.转化为线面垂直.支持定理①,////,//ababoab；②//aa；③//////配图助记baabbaabOaaaba（4）线线垂直：思考途径I.转化为相交垂直；II.转化为线面垂直；III.转化为线与另一线的射影垂直；IV.转化为线与形成射影的斜线垂直.支持定理①aabb；②所成角为900；③POaaPAaAO(三垂线及逆定理)；配图助记（5）线面垂直：思考途径I转化为该直线与平面内任一直线垂直；II转化为该直线与平面内相交二直线垂直；III转化为该直线与平面的一条垂线平行；IV转化为该直线垂直于另一个平行平面；V转化为该直线与两个垂直平面的交线垂直.支持定理①,,ababOllalb；②,laaal；③//aa；④//abba配图助记lbaOalaababPAOa（6）面面垂直：思考途径I.转化为判断二面角是直二面角；II.转化为线面垂直.支持定理①二面角900；②aa；③//aa配图助记16.2、求解空间角、距离和体积(一)求角：（步骤------Ⅰ.找或作平面角；Ⅱ.求角）⑴异面直线所成角的求法：①平移法：平移直线，构造三角形；②补形法：补成正方体、平行六面体、长方体等，发现两条异面直线间的关系.(理科还可用向量法，转化为两直线方向向量的夹角.)⑵直线与平面所成的角：①直接法（利用线面角定义）；②先求斜线上的点到平面距离h，与斜线段长度作比，得sin.（理科还可用向量法，转化为直线的方向向量与平面法向量的夹角.）⑶二面角的求法：①定义法：在二面角的棱上取一点（特殊点），作出平面角，再求解；②三垂线法：由一个半面内一点作（或找）到另一个半平面的垂线，用三垂线定理或逆定理作出二面角的平面角，再求解；③射影法：利用面积射影公式：cos'SS,其中为平面角的大小；【注】：对于没有给出棱的二面角，应先作出棱，然后再选用上述方法；（理科还可用向量法，转化为两个半平面法向量的夹角.）（二）求距离：（步骤------Ⅰ.找或作垂线段；Ⅱ.求距离）⑴两异面直线间的距离：一般先作出公垂线段，再进行计算；⑵点到直线的距离：一般用三垂线定理作出垂线段，再求解；⑶点到平面的距离：①垂面法：借助面面垂直的性质作垂线段（确定已知面的垂面是关键），再求解；②等体积法；（理科还可用向量法：||||nnABd.）⑷球面距离（步骤）：aa①求线段AB的长；②求球心角AOB的弧度数；③求劣弧AB的长.（三）求体积常规方法：直接法（公式法）、分割法、补形法、等积法(位置转换)、比例法(性质转换)等.