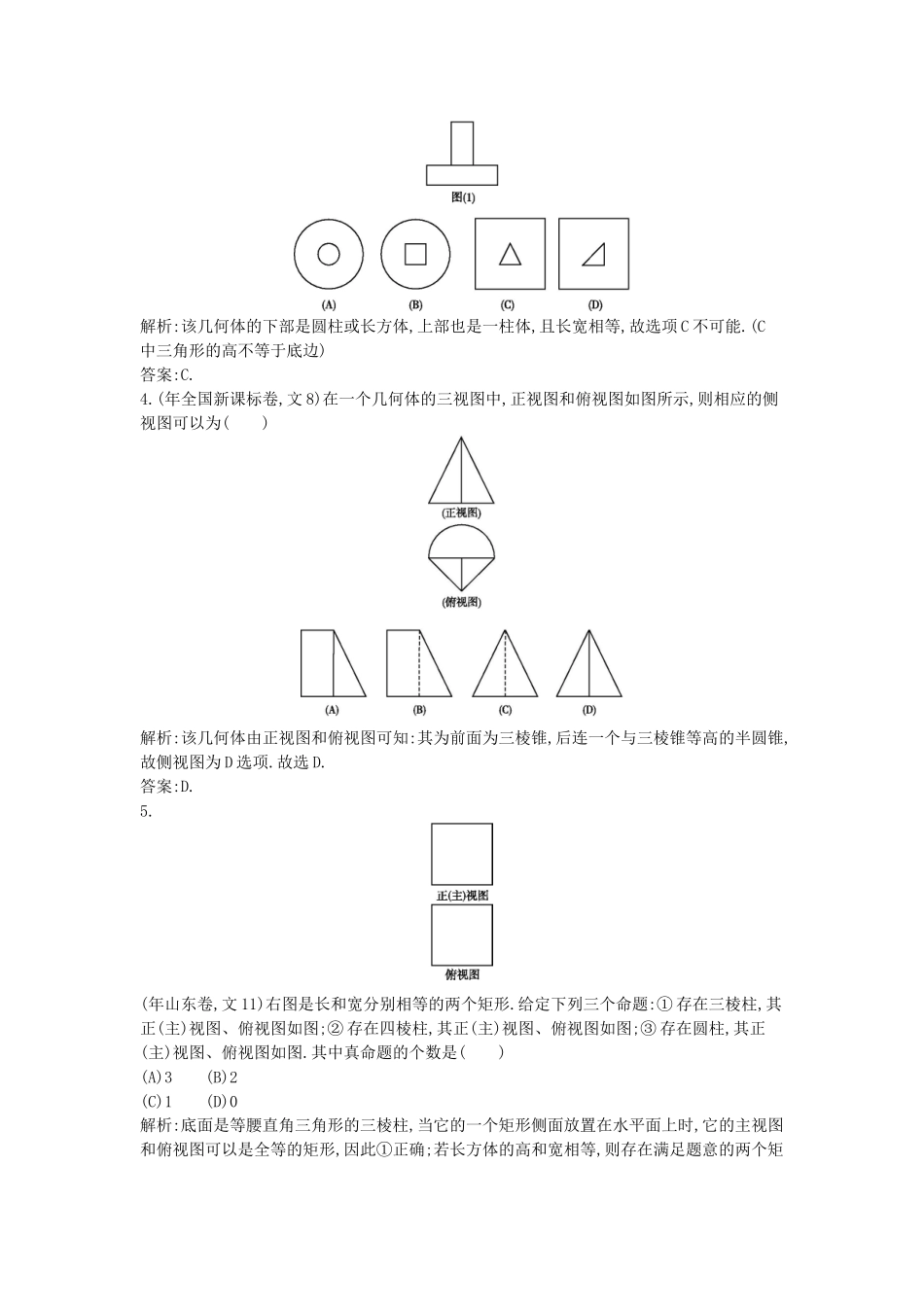
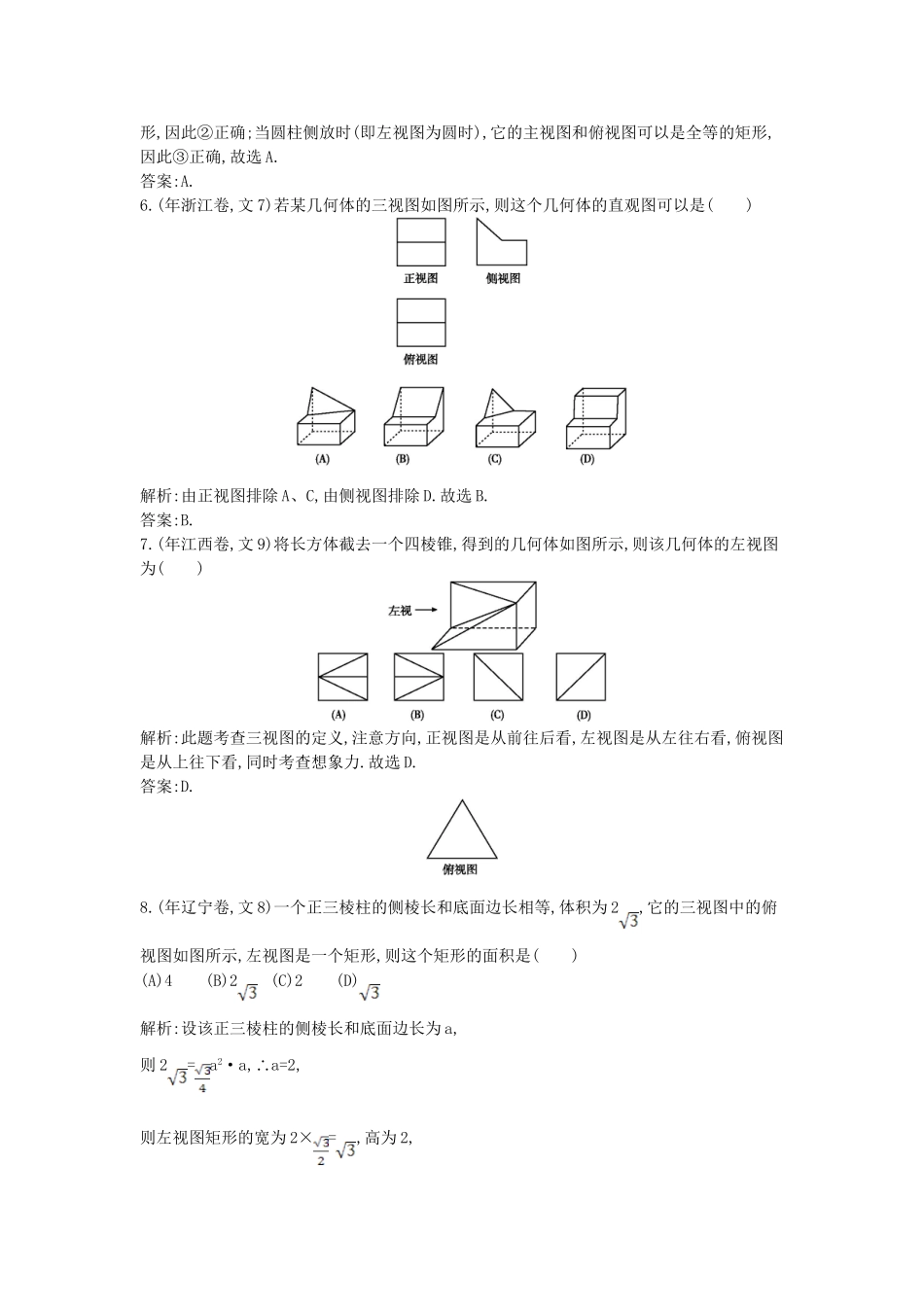
第一节空间几何体三视图的辨析考向聚焦高考的常考点,主要考查:(1)不同视图之间的关系;(2)由实物图画三视图.常以选择题形式出现,难度不大,所占分值5分备考指津(1)熟记三视图的绘图法则;(2)会由直观图画三视图;(3)能补全三视图,注意空间想象能力的训练1.(年福建卷,文4,5分)一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()(A)球(B)三棱锥(C)正方体(D)圆柱解析:一般地,圆柱的正视图是矩形,侧视图是矩形,而俯视图是圆.而球、正方体、三棱锥的三视图形状都相同,大小均相等是可以的,故选D.答案:D.2.(年陕西卷,文8,5分)将正方体(如图(1)所示)截去两个三棱锥,得到图(2)所示的几何体,则该几何体的左视图为()解析:因为从左面垂直光线在竖直平面上的正投影是正方形,其中D1A的正投影是正方形的对角线(实线),B1C的正投影被遮住是虚线,所以B正确.答案:B.本题主要考查空间图形的直观图与三视图,考查空间想象能力与逻辑推理能力.3.(年湖南卷,文4,5分)某几何体的正视图和侧视图均如图(1)所示,则该几何体的俯视图不可能是()解析:该几何体的下部是圆柱或长方体,上部也是一柱体,且长宽相等,故选项C不可能.(C中三角形的高不等于底边)答案:C.4.(年全国新课标卷,文8)在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()解析:该几何体由正视图和俯视图可知:其为前面为三棱锥,后连一个与三棱锥等高的半圆锥,故侧视图为D选项.故选D.答案:D.5.(年山东卷,文11)右图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱柱,其正(主)视图、俯视图如图;②存在四棱柱,其正(主)视图、俯视图如图;③存在圆柱,其正(主)视图、俯视图如图.其中真命题的个数是()(A)3(B)2(C)1(D)0解析:底面是等腰直角三角形的三棱柱,当它的一个矩形侧面放置在水平面上时,它的主视图和俯视图可以是全等的矩形,因此①正确;若长方体的高和宽相等,则存在满足题意的两个矩形,因此②正确;当圆柱侧放时(即左视图为圆时),它的主视图和俯视图可以是全等的矩形,因此③正确,故选A.答案:A.6.(年浙江卷,文7)若某几何体的三视图如图所示,则这个几何体的直观图可以是()解析:由正视图排除A、C,由侧视图排除D.故选B.答案:B.7.(年江西卷,文9)将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为()解析:此题考查三视图的定义,注意方向,正视图是从前往后看,左视图是从左往右看,俯视图是从上往下看,同时考查想象力.故选D.答案:D.8.(年辽宁卷,文8)一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,左视图是一个矩形,则这个矩形的面积是()(A)4(B)2(C)2(D)解析:设该正三棱柱的侧棱长和底面边长为a,则2=a2·a,∴a=2,则左视图矩形的宽为2×=,高为2,所以该矩形的面积为×2=2.故选B.答案:B.9.(年广东卷,文9)如图,△ABC为正三角形,AA'∥BB'∥CC',CC'⊥平面ABC且3AA'=BB'=CC'=AB,则多面体ABCA'B'C'的正视图(也称主视图)是()解析:正视图是从几何体的前面通过正投影得到的平面图形,故选D.答案:D.与三视图相关的空间几何体的表面积、体积考向聚焦高考的高频考点,主要考查:(1)通过三视图获取空间几何体特征的能力;(2)通过三视图求空间几何体的表面积、体积,从而考查学生的空间想象能力和计算能力.常以选择题、填空题形式出现,有时作为解答题第(1)问出现,难度中档,所占分值4~6分备考指津训练题型:由三视图(或三视图中的两种视图)求空间几何体的表面积、体积,加强识图能力的训练10.(年广东卷,文7,5分)某几何体的三视图如图所示,它的体积为()(A)72π(B)48π(C)30π(D)24π解析:本题主要考查三视图以及球与圆锥的体积问题,其体积为V=××π×33+×π×32×4=18π+12π=30π.答案:C.11.(年浙江卷,文3,5分)已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是()(A)1cm3(B)2cm3(C)3cm3(D)6cm3解析:本题主要考查了三视图的应用,根据三棱锥的体积公式V=××2×1×3=1,所以选A.答案:A.12.(年新课标全国卷,文7,5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为()(A)6(B)9(C)12(D)18解析:由题意知,V=××6×3×3=9.答案:B.13.(年新课标全国卷,文8,5分)平面...