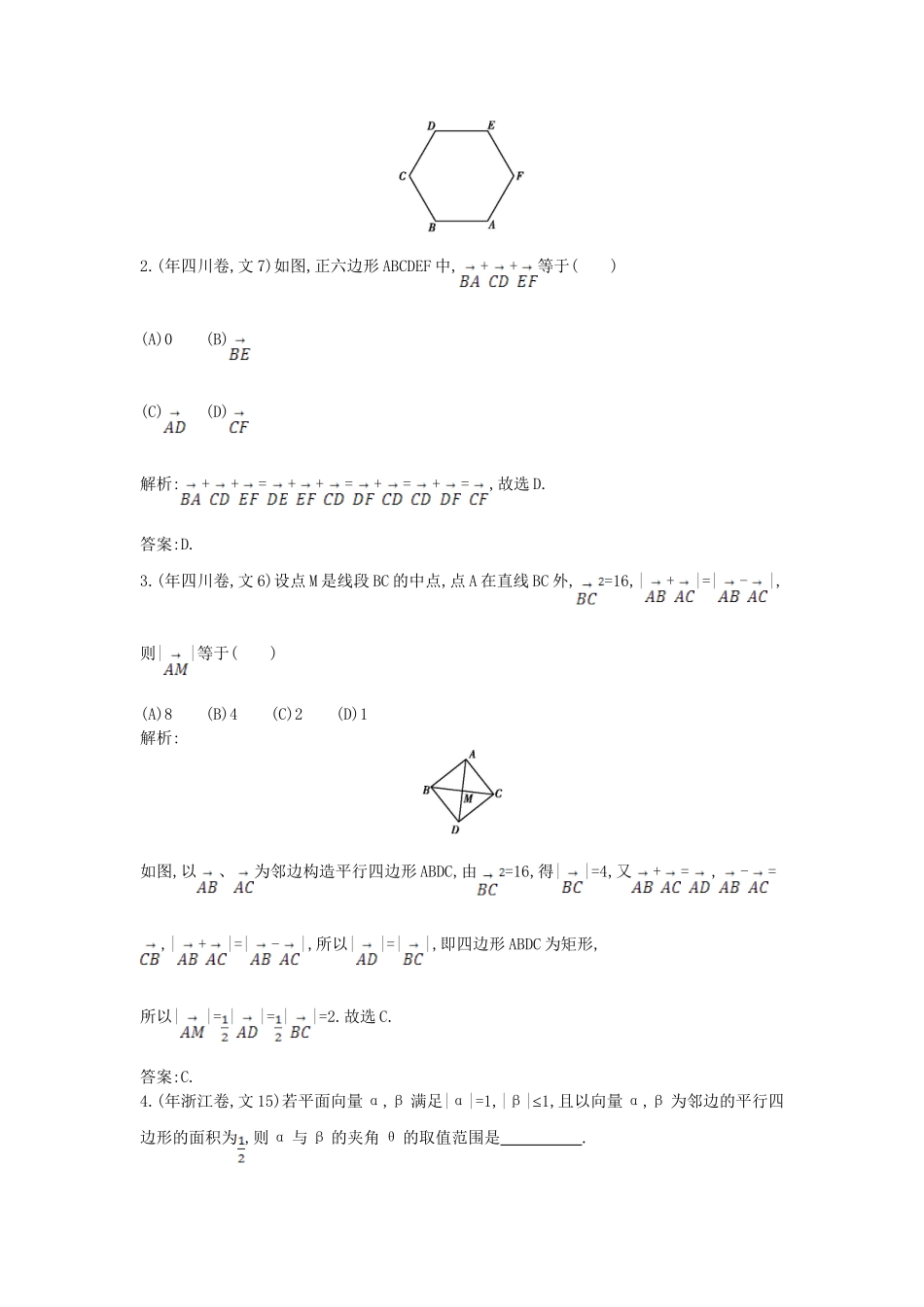
第一节平面向量的线性运算、平面向量基本定理向量的线性运算及其几何意义考向聚焦高考对本部分的考查较为重视,主要有两方面:(1)以平面图形为载体表达平面向量,借助向量表达数量关系与位置关系;(2)借助平面几何、解析几何等知识考查线性运算的法则及其几何意义.本部分常以客观题的形式出现,难度不大,所占分值为5分备考指津训练题型:(1)利用平行四边形法则或三角形法则进行平面向量的线性运算;(2)借助线性运算的几何意义与其他知识相结合求模或参数问题1.(年全国大纲卷,文9,5分)△ABC中,AB边的高为CD,若=a,=b,a·b=0,|a|=1,|b|=2,则等于()(A)a-b(B)a-b(C)a-b(D)a-b解析:由题意可得∠ACB=90°,且AB=,∴AD=AC×cosA=2×,∴AD=AB,∴=(-)=(a-b),故选D.答案:D.2.(年四川卷,文7)如图,正六边形ABCDEF中,++等于()(A)0(B)(C)(D)解析:++=++=+=+=,故选D.答案:D.3.(年四川卷,文6)设点M是线段BC的中点,点A在直线BC外,=16,|+|=|-|,则||等于()(A)8(B)4(C)2(D)1解析:如图,以、为邻边构造平行四边形ABDC,由=16,得||=4,又+=,-=,|+|=|-|,所以||=||,即四边形ABDC为矩形,所以||=||=||=2.故选C.答案:C.4.(年浙江卷,文15)若平面向量α,β满足|α|=1,|β|≤1,且以向量α,β为邻边的平行四边形的面积为,则α与β的夹角θ的取值范围是.解析:由已知得平行四边形的面积S=|α|·|β|sinθ=.∵|α|=1,∴sinθ=,又∵|β|≤1,∴sinθ=≥,又∵0≤θ≤π,∴≤θ≤.答案:[,]共线向量考向聚焦共线向量是很重要的概念之一,高考对共线向量的考查主要有两个方面:(1)两个向量共线的充要条件或以向量为载体求参数的值;(2)多与坐标运算相结合命题主要考查共线向量的判断和应用,难度不大,多以客观题为主,所占分值为5分左右5.(年浙江卷,文7,5分)设a,b是两个非零向量()(A)若|a+b|=|a|-|b|,则a⊥b(B)若a⊥b,则|a+b|=|a|-|b|(C)若|a+b|=|a|-|b|,则存在实数λ,使得b=λa(D)若存在实数λ,使得b=λa,则|a+b|=|a|-|b|解析:本题主要考查了平面向量的运算.A当等式成立时向量a和b共线方向相反不垂直;B当|a|<|b|时是错误的;C根据向量的平行四边形法则是正确的,D中当a|<|b|时是错误的,所以选C.答案:C.本题对于平面向量问题的设计新颖,容易对|a+b|=|a|-|b|的两边平方解题出现错误.6.(年山东卷,文12)设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若=λ(λ∈R),=μ(μ∈R),且+=2,则称A3,A4调和分割A1,A2.已知点C(c,0),D(d,0),(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是()(A)C可能是线段AB的中点(B)D可能是线段AB的中点(C)C,D可能同时在线段AB上(D)C,D不可能同时在线段AB的延长线上解析:因为平面上的点C,D调和分割点A,B,则由条件知=λ(λ∈R),=μ(μ∈R),且+=2.对A:若C为线段AB的中点,则λ=,所以=0,显然不存在μ,所以A是错误的,同理B也是错误的;对C:若C、D同时在线段AB上,则0<λ<1,0<μ<1,所以+>2,不符合条件;对D:若C、D同时在线段AB延长线上,则λ>1,μ>1,与+=2矛盾,故不可能,故选D.答案:D.7.(年北京卷,文11)已知向量a=(,1),b=(0,-1),c=(k,).若a-2b与c共线,则k=.解析:a-2b=(,3),∵a-2b与c共线,∴3=3k,∴k=1.答案:1平面向量基本定理的应用考向聚焦高考对平面向量基本定理的考查比较全面,主要体现在:(1)以平面向量基本定理为基石,利用一组基底表示相关向量;(2)平面向量基本定理多与向量的数量积、坐标运算相结合,通常以三角形或四边形为载体命题,难度不大,主要以客观题为主,所占分值约为5分8.(年湖北卷,文8)已知△ABC和点M满足++=0,若存在实数m使得+=m成立,则m等于()(A)2(B)3(C)4(D)5解析:由++=0,得点M为△ABC的重心,∴+=3,∴m=3,故选B.答案:B.9.(年大纲全国卷Ⅱ,文10)△ABC中,点D在边AB上,CD平分∠ACB.若=a,=b,|a|=1,|b|=2,则等于()(A)a+b(B)a+b(C)a+b(D)a+b解析:如图,∵CD平分∠ACB,∴=.又∵=a,=b,|a|=1,|b|=2,∴=2,∴=+=a+=a+(-)=a+(b-a)=a+b,故选B.答案:B.