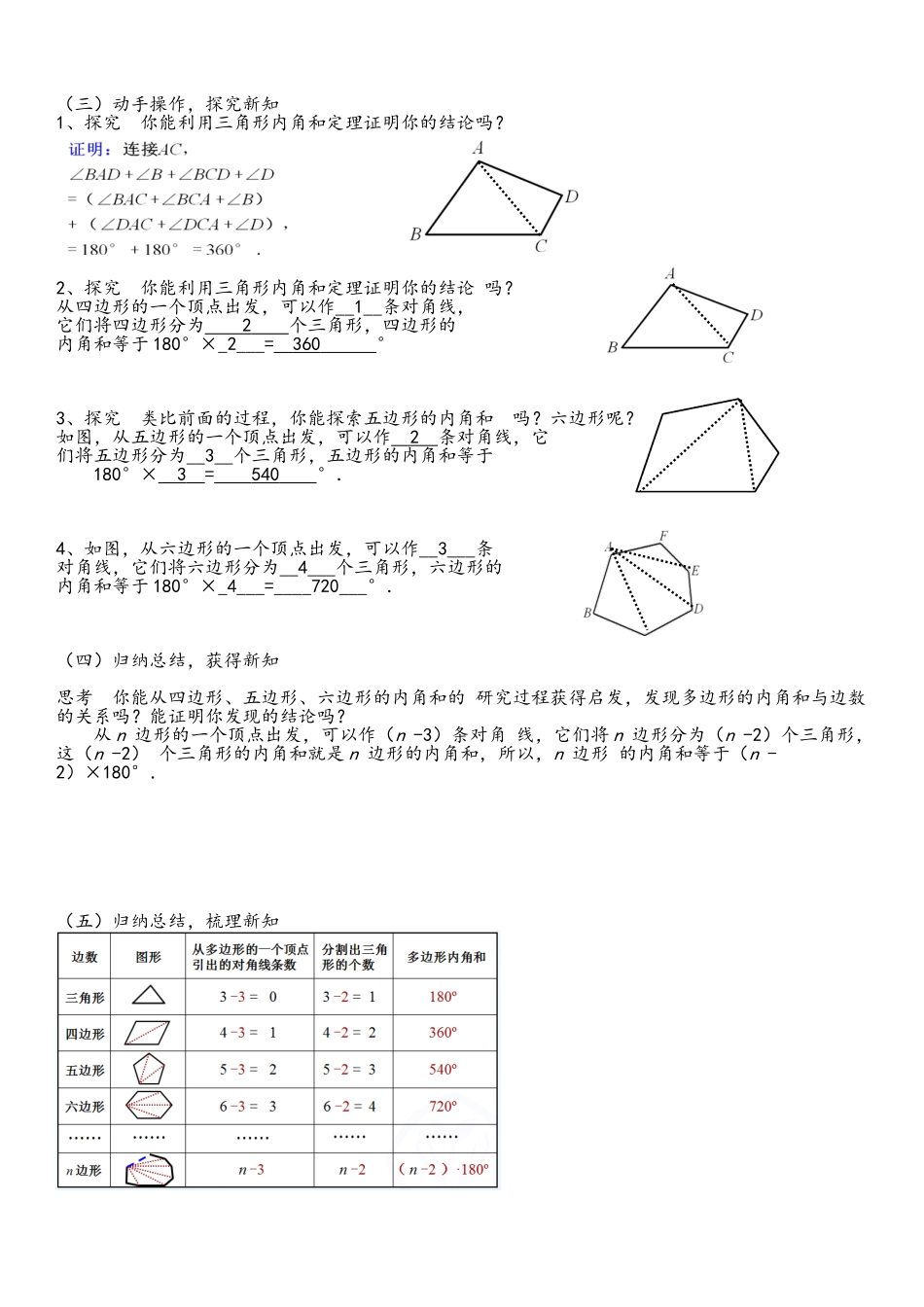
多边形及其内角和(第1课时)教案高志军一、学习目标:1.了解多边形的有关概念,感悟类比方法的价值.2.探索并证明多边形内角和公式,体会化归思想和从具体到抽象的研究问题方法.3.运用多边形内角和公式解决简单问题.二、学习重点:多边形内角和公式的探索与证明过程.三、教学过程(一)创设情境,导入新知1、问题你能从图中想象出几个由一些线段围成的图形吗?2、多边形的定义:在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.(二)创设情境,观察新知1、如图,从五边形ABCDE的顶点A出发共有几条对角线?2、观察你能说出这两个图形的异同点吗?凸四边形凹四边形3、想一想正方形的边、角有什么特点?各个角都相等,各条边都相等的多边形叫做正多边形.4、回忆长方形、正方形的内角和等于______.5、思考任意一个四边形的内角和是否也等于360°呢?(三)动手操作,探究新知1、探究你能利用三角形内角和定理证明你的结论吗?2、探究你能利用三角形内角和定理证明你的结论吗?从四边形的一个顶点出发,可以作__1__条对角线,它们将四边形分为2个三角形,四边形的内角和等于180°×_2___=360°3、探究类比前面的过程,你能探索五边形的内角和吗?六边形呢?如图,从五边形的一个顶点出发,可以作2条对角线,它们将五边形分为__3__个三角形,五边形的内角和等于180°×3=540°.4、如图,从六边形的一个顶点出发,可以作__3___条对角线,它们将六边形分为__4___个三角形,六边形的内角和等于180°×_4___=____720___°.(四)归纳总结,获得新知思考你能从四边形、五边形、六边形的内角和的研究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?从n边形的一个顶点出发,可以作(n-3)条对角线,它们将n边形分为(n-2)个三角形,这(n-2)个三角形的内角和就是n边形的内角和,所以,n边形的内角和等于(n-2)×180°.(五)归纳总结,梳理新知(六)动脑思考,例题解析例1填空:(1)十边形的内角和为1440度.(2)已知一个多边形的内角和为1080°,则它的边数为___8___.例2如果一个四边形的一组对角互补,那么另一组对角有什么关系?解:如图,四边形ABCD中,∠A+∠C=180°.∵∠A+∠B+∠C+∠D=(4-2)×180°=360°,∴∠B+∠D=360°-(∠A+∠C)=360°-180°=180°.如果四边形的一组对角互补,那么另一组对角也互补.(七)课堂小结(1)本节课学习了哪些主要内容?(2)我们是怎样得到多边形内角和公式的?(3)在探究多边形内角和公式中,连接对角线起到什么作用?(八)布置作业教科书习题11.3第1、2、4、5题.