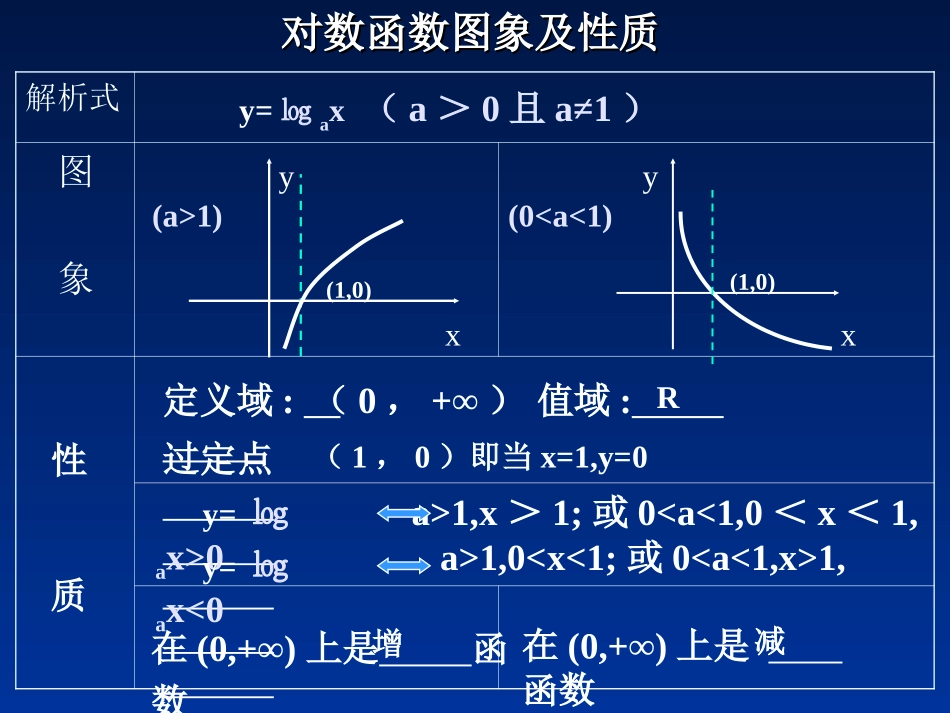
对数函数对数函数((二二))对数函数图象及性质的应用对数函数图象及性质的应用解析式图象对数函数图象及性质对数函数图象及性质定义域:值域:过定点性质在(0,+∞)上是函数在(0,+∞)上是函数xy(a>1)xy(0
0y=㏒ax<0a>1,x>1;或01,01,例1:比较下列各组中两个值的大小:(1)log23,log23.5(2)log0.71.6,logo.71.8(3)log67,log76(4)log31.2,log20.8解:(1)考察对数函数y=log2x,因为2>1,3<3.5所以log23log0.71.8(3)log∵67>log66=1,log76log76(4)∵log31.2>log31=0,log20.8log20.8总结:比较对数的大小,一般利用对数函数单调性得出同底对数的大小关系。若底数不同,可把1或0作中间值进行比较。练习:1、比较60.7,0.76,log0.76的大小。>>2、将,,由小到大排列。log0.80.7log0.91.10.91.13、解不等式20.20.2log(23)log(31)xxx0.91.10.7log0.9log0.81.1117{|1}2xx5、函数y=lg(x2-3x+2)的定义域为F,y=lg(x-1)+lg(x-2)的定义域为G,那么()AFGBFGCFGDGF6、设,则实数a的取值范围是()2log13a220133220133AaBaCaaDa或4、函数的图像恒过点A,则A点坐标为。log(1)1ayx(2,1)7、函数y=logax,y=logbx,y=logcx,y=logdx的图象如图所示,则a,b,c,d从大到小的排列为。Xy0y=1y=logaxy=logbxy=logcxy=logdxc0且a≠1,∴函数t=2-ax是减函数。由y=loga(2-ax)在[0,1]上是减函数,知y=logat是增函数。∴a>1.再考虑[0,1]应在定义域内,定义域:2-ax>0,得到ax<2,x<2/a。2/a>1,∴a<2。∴1解得或3又a=-1,f(x)=0满足题意;a=1,不合题意。实数a的取值范围是:5,3-,-1综合:2、已知函数,若f(x)的值域为R,求实数a的取值范围。22()lg111fxaxax解:依题意22111taxax能取到(0,+∞)上任何值,则f(x)的值域为R。当a2-1≠0时,其充要条件是:222101410aaa5:1