2.1.3向量的减法VIP免费

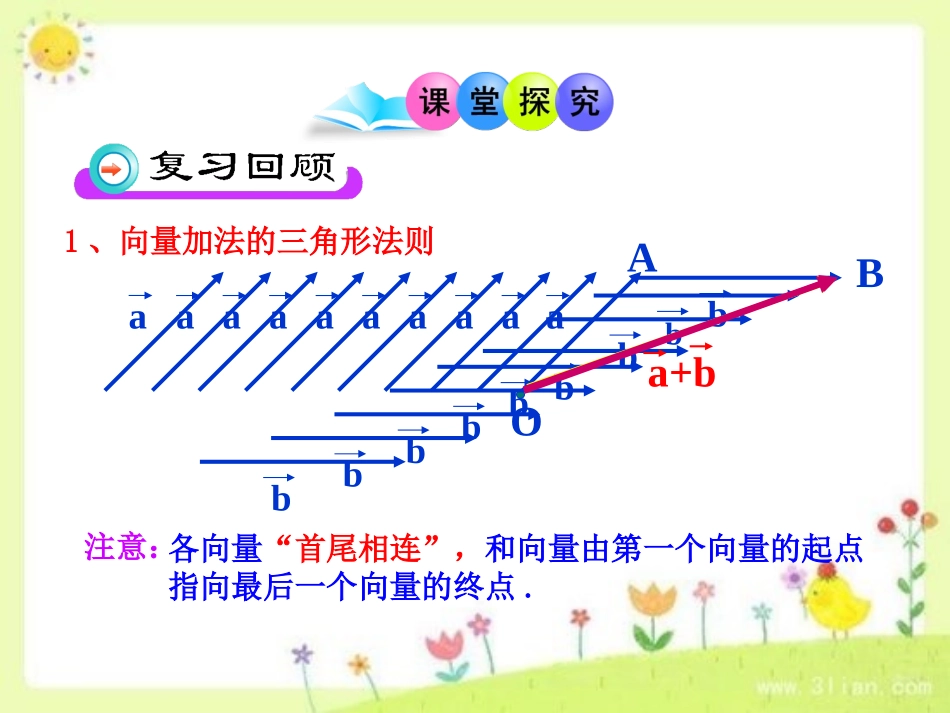
2.1.3向量的减法实数之间有加减乘除四则运算，上一节我们学习了向量的加法，那么有没有向量的减法呢？让我们一起来研究！1、向量加法的三角形法则baOaaaaaaaabbbbbbbBbaA注意：a+b各向量“首尾相连”，和向量由第一个向量的起点指向最后一个向量的终点.baAaaaaaaaabbbBbaDaCba+b注意：（1）起点相同；（2）共线向量不适用.(1)2.3AAABCDADBCABDCAAC��在平面内任取一点；（）以点为起点以向量、为邻边作平行四边形即＝＝，＝＝；（）则以点为起点的对角线作法：＝ababab.2、向量加法的平行四边形法则说明：１.与长度相等、方向相反的向量，叫做的相反向量.２.零向量的相反向量仍是零向量.３.任一向量和它相反向量的和是零向量.-(-),abab求两个向量差的运算叫向量的减法.：定表示义：bb1-(-)______(2)(-)_____(-)______(3),______,______,______aaaaaababab（）如果互为相反的向量，那么a00ba0,,-abab��已知根据减法的定义，如何作出呢？abOAabBbCDba,,-.abbaab平移向量使它们起点相同，那么的终点指向的终点的向量就是方法：二、向量减法的三角形法则OABabba1O在平面内任取一点2,OAaOBb�作3BAab�则向量.注意：1、两个向量相减，则表示两个向量起点的字母必须相同2、差向量的终点指向被减向量的终点•特殊情况1.共线同向2.共线反向abBACababABCab1.().ABCDABADACDB��例已知平行四边形，＝，＝，用、分别表示向量，如下图所示abababADBCACDB,ACABAD.DBAB-AD.��边连则减义接、由向量和的平行四形法，有＝＝依法定得解：＝aba-bADBCab2.--.例已知向量、、与，求，(如下图所示)abcdabcdOAOBBA-OA-OBBA;OCOD,DCOC-ODDC.����则则作＝，＝，作，＝作＝＝作，解：，ababcdc-dabcdadcbabcd1.,,,,-,-.abcdabcd��如图，已知向量求作向量abcdOABCDabcd��(1)--ABACBDCD�化简-:-0CBBDCDCDCD�解原式(2)OAOCBOCO�化简()()(-)0:OABOOCCOOAOBBA��解原式2.化简下列各式ABCDabcO.bcDAOCOCCBOBbcaOBABOBBAOA����证明：3.,,,,-ABCDABaDAbOCcbcaOA����如图平行四边形证明：一、知识1．理解相反向量的概念2.理解向量减法的定义3.正确熟练地掌握向量减法的三角形法则二、重点向量减法的定义、向量减法的三角形法则长期的心灰意懒以及烦恼足以致人于贫病枯萎。——布朗