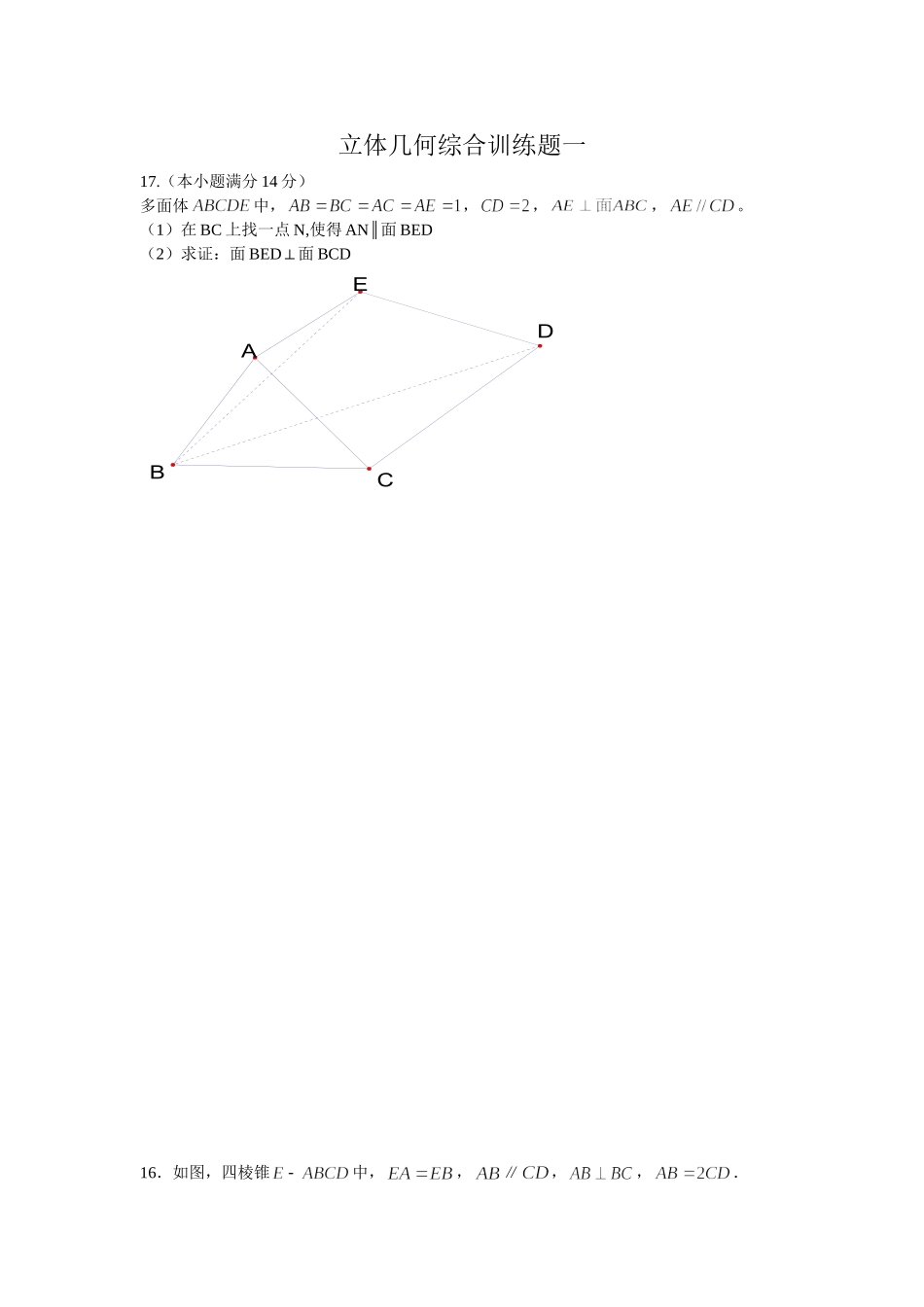
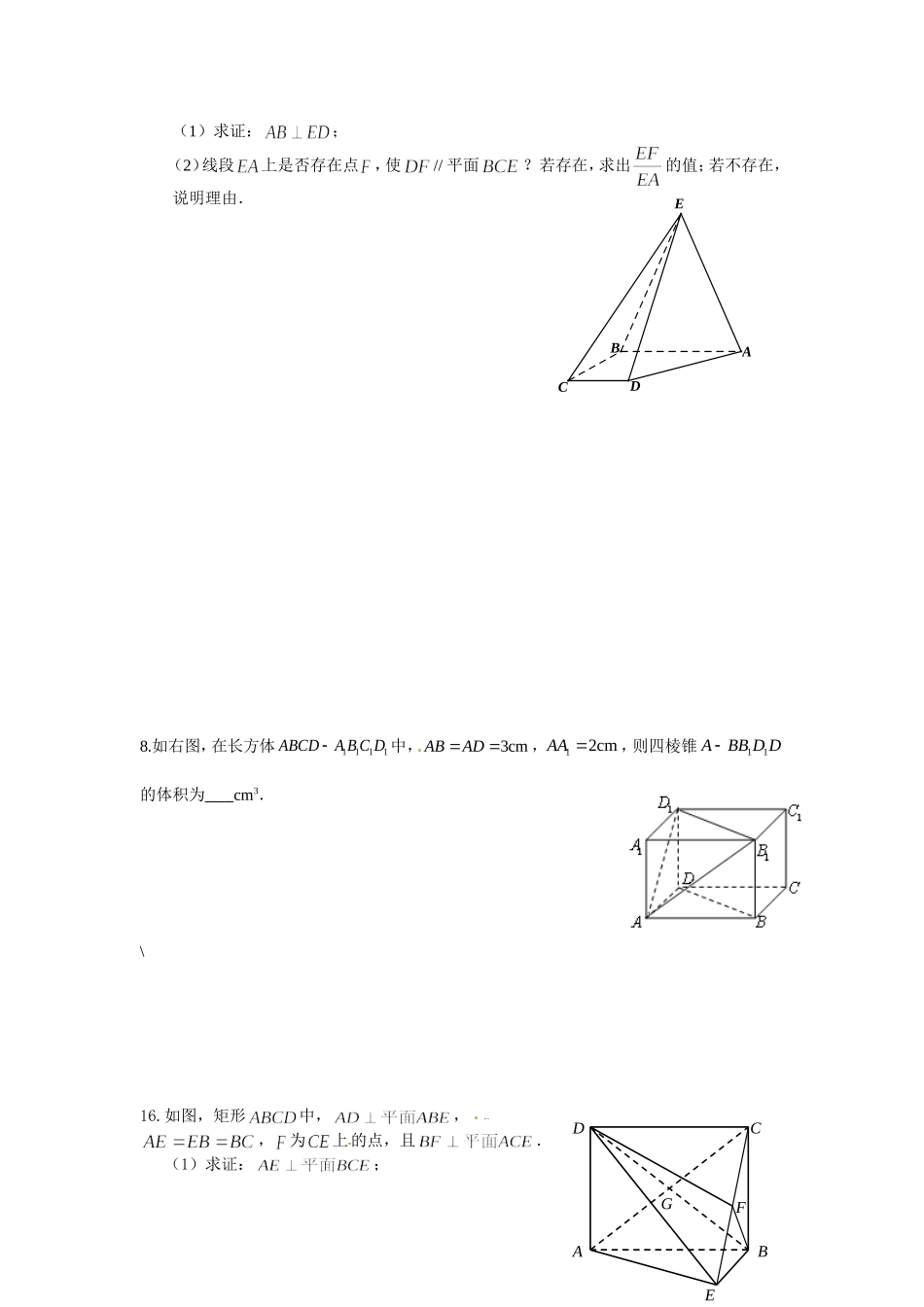
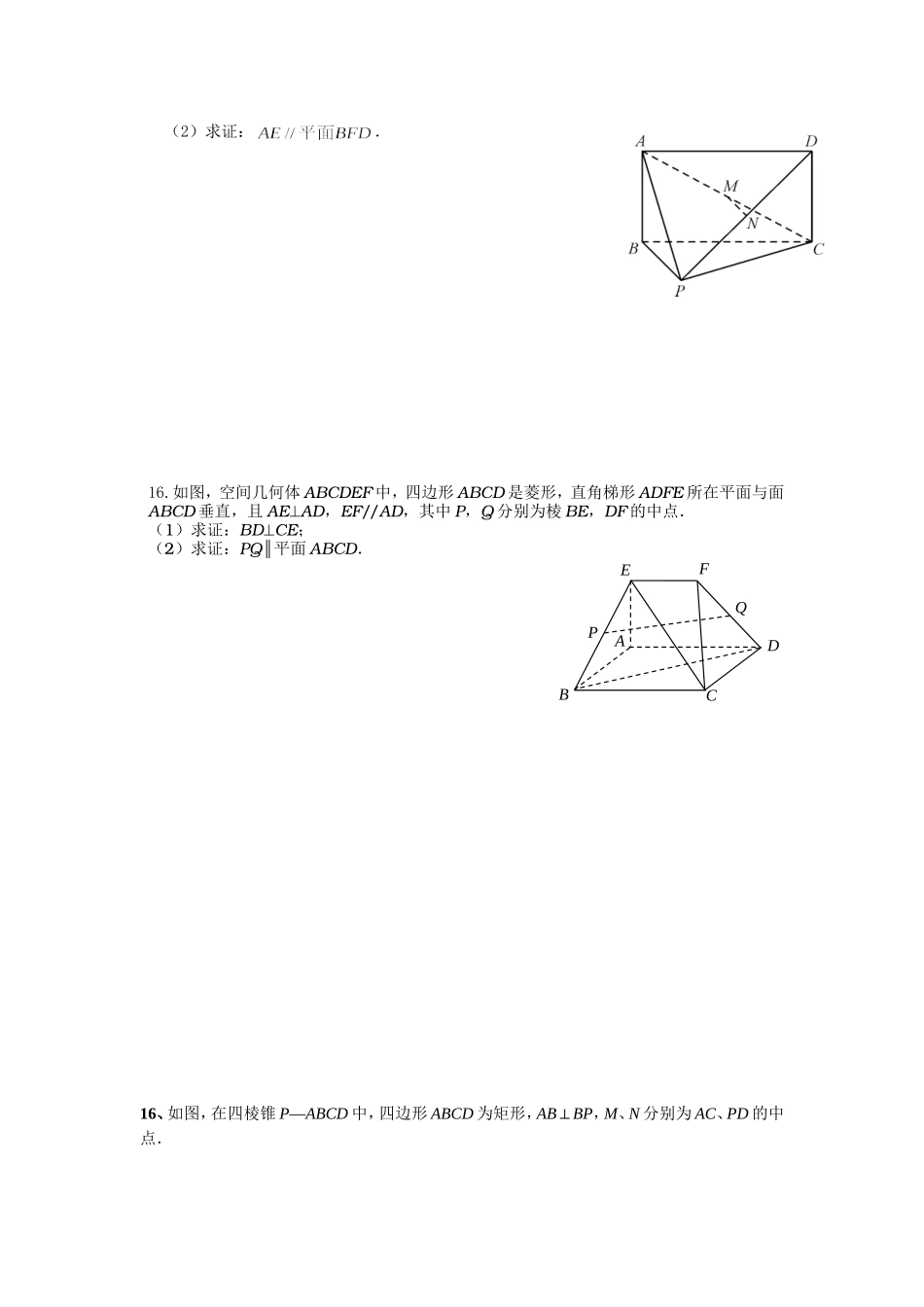
立体几何综合训练题一17.(本小题满分14分)多面体中,,,,。(1)在BC上找一点N,使得AN∥面BED(2)求证:面BED⊥面BCDEDABC16.如图,四棱锥中,,∥,,.ADCBE(1)求证:;(2)线段上是否存在点,使//平面?若存在,求出的值;若不存在,说明理由.8.如右图,在长方体1111ABCDABCD中,3cmABAD,12cmAA,则四棱锥11ABBDD的体积为cm3.\16.如图,矩形中,,w.w.w.k.s.5.u.c.o.m,为上的点,且.(1)求证:;ABCDEFG(2)求证:.16.如图,空间几何体ABCDEF中,四边形ABCD是菱形,直角梯形ADFE所在平面与面ABCD垂直,且AEAD,EF//AD,其中P,Q分别为棱BE,DF的中点.(1)求证:BDCE;(2)求证:PQ∥平面ABCD.16、如图,在四棱锥P—ABCD中,四边形ABCD为矩形,AB⊥BP,M、N分别为AC、PD的中点.ABCDEFPQ求证:(1)MN∥平面ABP;(2)平面ABP⊥平面APC的充要条件是BP⊥PC.10.已知正三棱锥PABC,点,,,PABC都在半径为3的球面上,若,,PAPBPC两两相互垂直,则球心到截面ABC的距离为.16.如图,四棱锥PABCD的底面为矩形,且2,1ABBC,,EF分别为,ABPC的中点.(1)求证:EF∥平面PAD;(2)若平面PAC⊥平面ABCD,求证:平面PAC⊥平面PDE.6.如图所示的“双塔”形立体建筑,已知和是两个高相等的正三棱锥,四点在同一平面内.要使塔尖之间的距离为m,则底边的长为m.(第16题)ABCDEFPPQABCD第6题图16.(本题满分14分)如图,正方形所在的平面与三角形所在的平面交于,平面,且.(1)求证:平面;(2)求证:平面平面;立体几何综合训练题一参考答案17.(本小题满分14分)多面体中,,,,。(1)在BC上找一点N,使得AN∥面BED(2)求证:面BED⊥面BCDABCDE(第16题图)ADCBEEDABC17、证明:(1)令BC中点为N,BD中点为M,连结MN、ENMN 是△ABC的中位线∴MNCD…………………………2∥分由条件知AECDMNAE∥∴∥又MN=CD=AE∴四边形AEMN为平行四边形ANEM…………………………4∴∥分AN 面BED,EM面BEDAN∴∥面BED……………………6分(2) AE⊥面ABC,AN面ABCAEAN∴⊥又 AECD,ANEMEMCD………………8∥∥∴⊥分N 为BC中点,AB=ACANBC∴⊥EMBC………………………………………………10∴⊥分EM∴⊥面BCD…………………………………………12分EM 面BED∴面BED⊥面BCD……14分16.如图,四棱锥中,,∥,,.(1)求证:;(2)线段上是否存在点,使//平面?若存在,求出的值;若不存在,说明理由.16.解:(1)证明:取中点,连结,.因为,所以.……………2分因为∥,,所以∥,.又因为,所以四边形为矩形,所以.…………4分因为,所以平面.…………6分所以.…………7分(2)解:点满足,即为中点时,有//平面.…………8分证明如下:取中点,连接,.……………9分因为为中点,所以∥,.因为∥,,所以∥,.所以四边形是平行四边形,所以∥.……………12分因为平面,平面,……………13分所以//平面.………14分8.如右图,在长方体1111ABCDABCD中,3cmABAD,12cmAA,则四棱锥11ABBDD的体积为cm3.16.如图,矩形中,,w.w.w.k.s.5.u.c.o.m,为上的点,且.(1)求证:;(2)求证:.16.如图,空间几何体ABCDEF中,四边形ABCD是菱形,直角梯形ADFE所在平面与面ABCD垂直,且AEAD,EF//AD,其中P,Q分别为棱BE,DF的中点.(1)求证:BDCE;(2)求证:PQ∥平面ABCD.ABCDEFGABCDEFPQ16、如图,在四棱锥P—ABCD中,四边形ABCD为矩形,AB⊥BP,M、N分别为AC、PD的中点.求证:(1)MN∥平面ABP;(2)平面ABP⊥平面APC的充要条件是BP⊥PC.16.证明:(1)连接BD,由于四边形ABCD为矩形,则BD必过点M(1分)又点N是PD的中点,则BPMN//,(2分)MN面ABPBP面ABP//MN面ABP(4分)(2)充分性:由“BP⊥PC.”“平面ABP⊥平面APC”BCABBPAB,,BP面PBC,BC面PBCBBCBPAB面PBC……………………………(6分)PC面PBCPCAB……………………..(7分)又BPPC,BPAB,是面ABP内两条相交直线PC面ABPPC面APC…………………………(9分)面ABP面APC………………………..(10分)必要性:由“平面ABP⊥平面APC”“BP⊥PC.”过B...