一次函数的图象2VIP免费

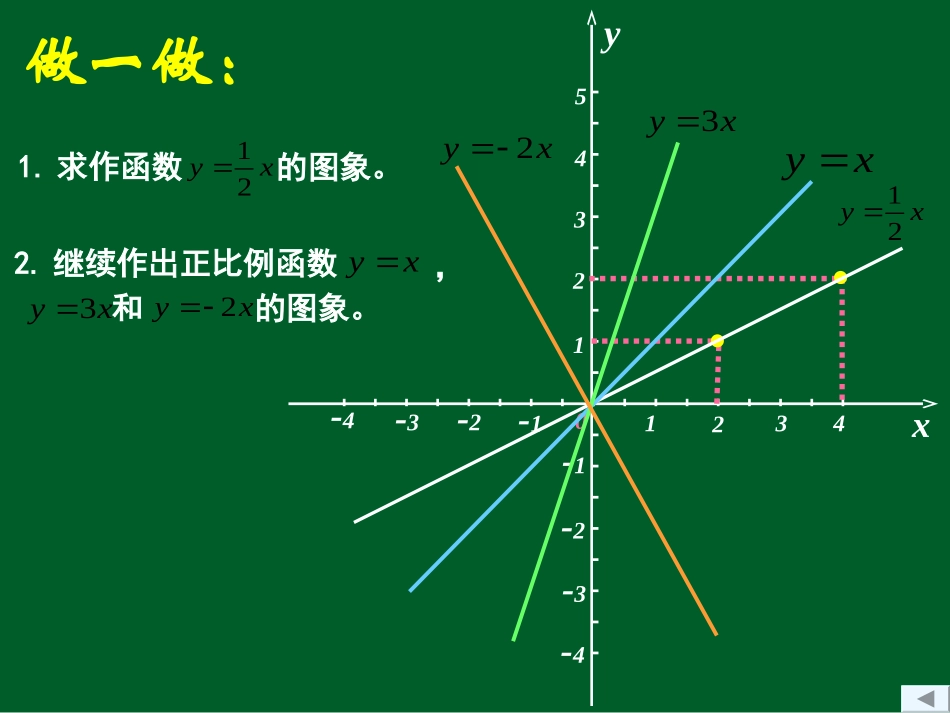
一次函数的图象第二课时冯卯镇欧峪小学李涛复习：1.把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标，在直角坐标系内描出它的对应点，所有的这些点组成的图形叫做该函数的图象。2.一次函数y=kx+b的图象是什么图形？你是通过确定几个对应点来作一次函数图象的呢？做一做：1.求作函数xy21的图象。2.继续作出正比例函数，xyxy3和xy2的图象。x1234-1y12345-1-2-3-4-2-3-40xy21xyxy3xy2小组议一议：，1.观察在同一直角坐标系中的这四个正比例函数图象：直线xy21，xy和xy3xy2yx123123-1-2-1-20xy3xy2合作交流、小组讨论：⑴正比例函数y=kx的图象有什么特点？⑵你作正比例函数y=kx的图象时描了几个点？⑶直线xy21xyxy3和，中哪一个与x轴正方向所成的锐角最大？哪一个与x轴正方向所成的锐角最小？xy34⑷猜一猜：直线xy51，，xy2xy7和中，哪一个与x轴正方向所成的锐角最大？哪一个与x轴正方向所成的锐角最小？xy21xyxy51xy7归纳总结：正比例函数y=kx图象的性质1.正比例函数y=kx的图象都是经过坐标原点（0，0）的一条直线；2.利用坐标原点（0，0），只需再确定另一个点，就可以作出正比例函数y=kx的图象。做一做：1.在同一直角坐标系中分别作出正比例函数xy5和xy的图象。yx123123-1-2-1-20xy5xy2xy2.在上题的直角坐标系中再作出一次函数2xy22xy和的图象。22xy1.你在作正比例函数的图象时描了几个点？而在作一次函数的图象时又描了几个点呢？议一议：2.观察函数图象，在上述四个函数中，随着x的值的增大，y的值分别又是如何变化的？yx123123-1-2-1-20xy5xy2xy22xy归纳总结：一次函数y=kx+b（b≠0）的性质在一次函数y=kx+b中当k>0时，y的值随着x值的增大而增大；当k<0时，y的值随着x值的增大而减小。随堂练习：1.下列一次函数中，y的值随着x值的增大而增大的有y的值随着x值的增大而减小的有；910xy（A）（D）（C）45xy（B）23.0xyxy32；为什么？（C）（A）（B）（D）2.写出m的3个值，使相应的一次函数212xmy的值都是随着x的增大而减小。分析：要使得一次函数bkxy的值都是随着2m<1而减小，则必须有k<0，即2m–1<0，所以x的增大yx123123-1-2-1-20xy5xy2xy22xy想一想：⑴X从0开始逐渐增大时，22xyxy5和哪一个的值先达到20？这说明了什么？⑵直线xy和2xy的位置关系如何？⑶直线22xy和2xy的位置关系如何？⑷猜一猜：a.直线xy31和131xy的位置关系如何？b.直线131xy和131xy的位置关系如何？c.直线131xy和12xy的位置关系如何？平行相交平行平行相交今天我们学会了…1.正比例函数的图象和性质2.一次函数的性质1下列函数,y的值随着x值的增大如何变化xyxyxyxy)32()4(45)3(23.0)2(910)1(2．y=x+1与坐标轴的交点坐标？3．y=(-3k+1)x+2k-1的图象经过原点，确定k的值？４．写出m的3个值，使相应的一次函数y=(2m-1)x+2的值都是随着x值的增大而减小.