26.1二次函数(第5课时).1二次函数(第5课时)VIP免费

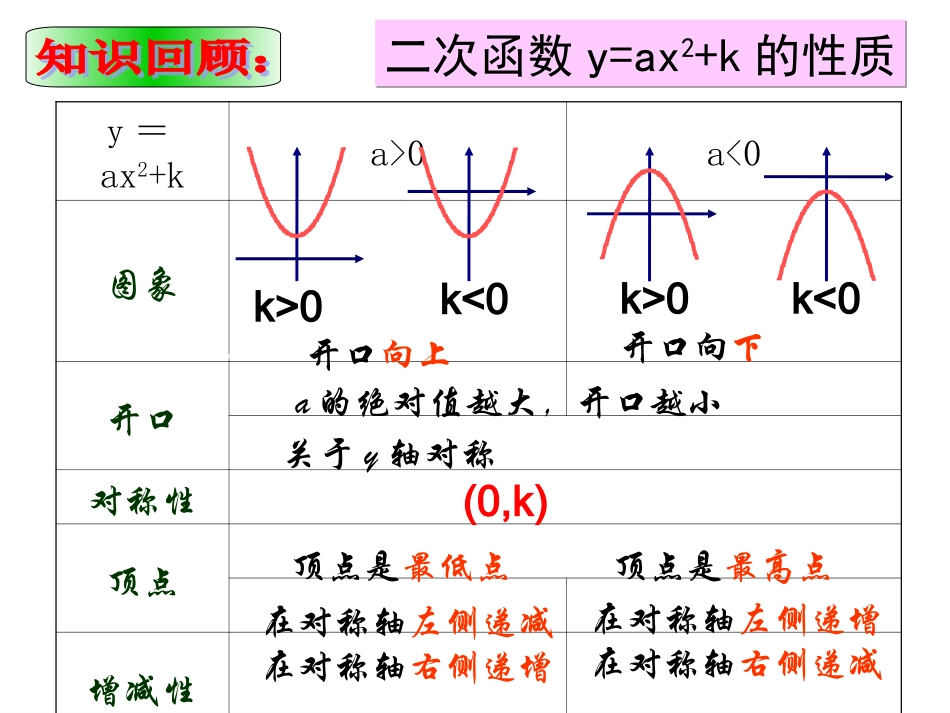
－222464－48212yx22yx2yxy＝ax2+ka>0a<0图象开口对称性顶点增减性二次函数y=ax2+k的性质二次函数y=ax2+k的性质开口向上开口向下a的绝对值越大，开口越小关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减在对称轴右侧递增在对称轴左侧递增在对称轴右侧递减k>0k<0k<0k>0(0,k)学科网y＝a(x-ｈ)2a>0a<0图象开口对称性顶点增减性二次函数y=a（x-ｈ）2的性质二次函数y=a（x-ｈ）2的性质开口向上开口向下a的绝对值越大，开口越小直线ｘ＝ｈ顶点是最低点顶点是最高点在对称轴左侧递减在对称轴右侧递增在对称轴左侧递增在对称轴右侧递减h>0h<0h<0h>0(ｈ,0)二次函数二次函数yy==axax22与yy==aa((xx––hh))22的关系的关系..当h>0时,向右平移当h<0时,向左平移yy==axax22yy==aa((x–h)x–h)22问题1：如何由y=-x2的图象得到y=-x2-3的图象。并说明后者图象的顶点，对称轴，增减性。问题2：如何由y=2x2的图象得到y=2(x-3)2的图象。并说明后者图象的顶点，对称轴，增减性。Z.x.x.K?问题3：把二次函数y=3(x-1)2加上+2所得函数y=3(x-1)2+2的图象是怎样的呢？26.1.2二次函数y=a(x-h)2+K的图象和性质（五）例3(1)画出函数的图象，解：作函数的图象：21112yx21112yx－22－2－4－64－4x···－4－3－2－1012·········21112yx－5.5－1.5－3－1－1.5－5.5－3抛物线的开口方向向下、对称轴是x=－1，顶点是（－1，－1）．21112yx把抛物线向下平移1个单位，再向左平移1个单位，就得到抛物线212yx21112yx例3:(2)指出它的开口方向、对称轴及顶点．(3)抛物线经过怎样的变换可以得到抛物线212yx21112yx－22－2－4－64－44)2(212xy抛物线怎样移动就可以得到抛物线？221xy?4)2(212xy怎样移动可以得到抛物线2222()_________()yaxhkyaxyaxyaxhk一般地，抛物线与形状，位置。把抛物线向上（下）向左（右）平移，可以得到抛物线。平移的方向、距离要根据_____的值来决定。。）顶点坐标是（；）对称轴是直线（；，开口；当时，开口）当（有如下特点：抛物线______3____2___0____01)(2aakhxay相同不同向上向下x=h（h，k）h、k二次函数y=a(x-h)2+k(a≠0)的图象和性质抛物线顶点坐标对称轴开口方向增减性最值向上向下在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.hk，hk，xh直线xh直线,xhk当时最小值为xhk当时，最大值为y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)1、说出下列抛物线的开口方向、对称轴及顶点：.62547343213253212222）（）；（）（）（；）（）；（）（）（xyxyxyxy开口向上对称轴是x=-3顶点是（-3，5）开口向下对称轴是x=1顶点是（1，-2）开口向上对称轴是x=3顶点是（3，7）开口向下对称轴是x=-2顶点是（-2，-6）2.指出下列函数图象的开口方向对称轴和顶点坐标及最值:3．对于二次函数y=3(x+1)2,当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?二次函数y=-3(x-1)2+4呢?211.y=2x+3-,2212.y=-x+1-5.3Zx.xk例4要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？如图建立直角坐标系例4要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管应多长？解：以池中心为原点，竖直安装的水管为y轴，与水管垂直的为x轴建立直角坐标系．由于在距池中心的水平距离为1m时达到最高，高度为3m，则设抛物线的解析式为：y=a（x-1）2+3，．因为点（3，0）在抛物线上，所以代入（3，0）求得：a=-将a值代入得到抛物线的解析式函数解析式为：y=-（x-1）2+3．3414=2.25．令x=0，则y=94故水管长为2.25m．