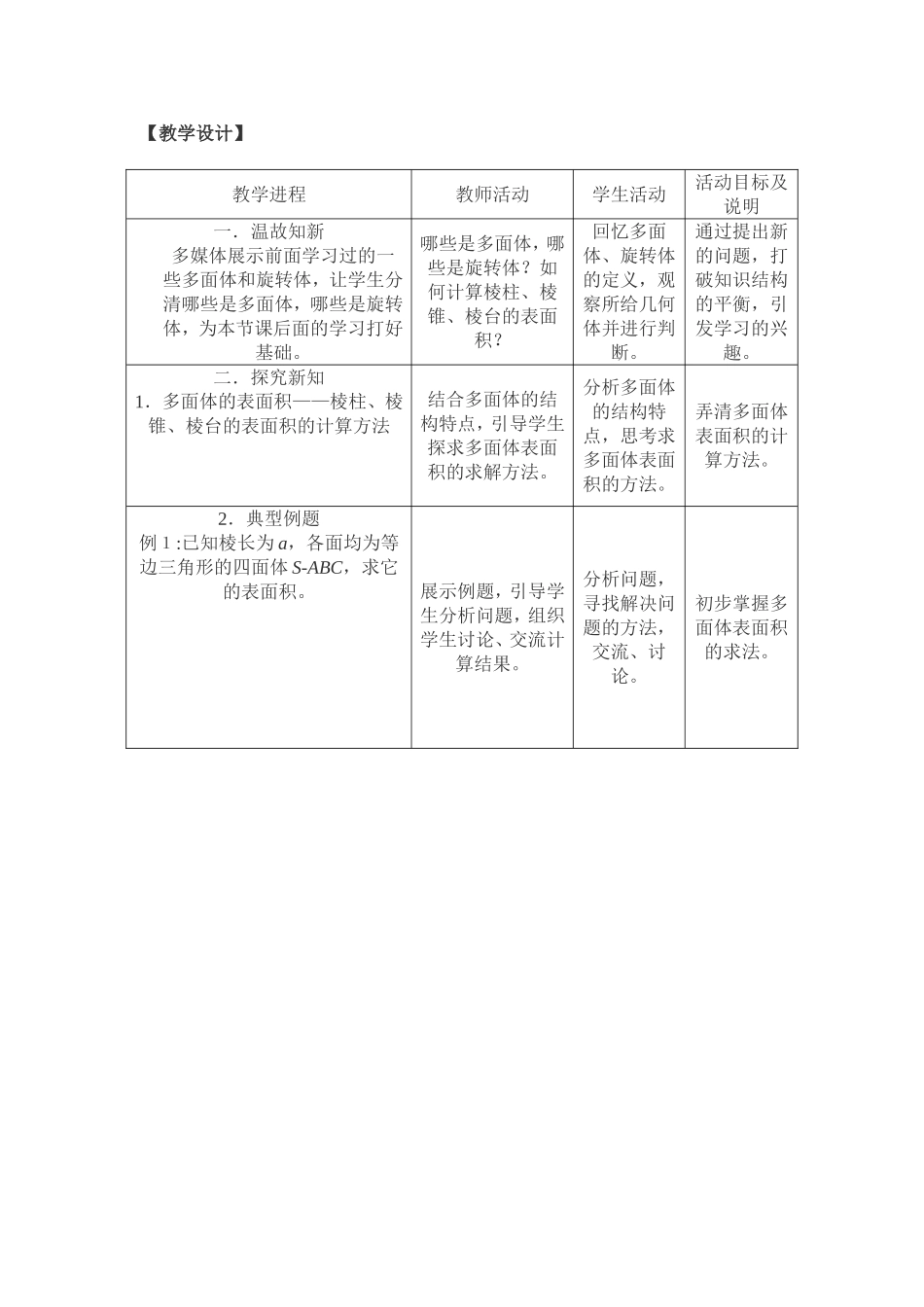
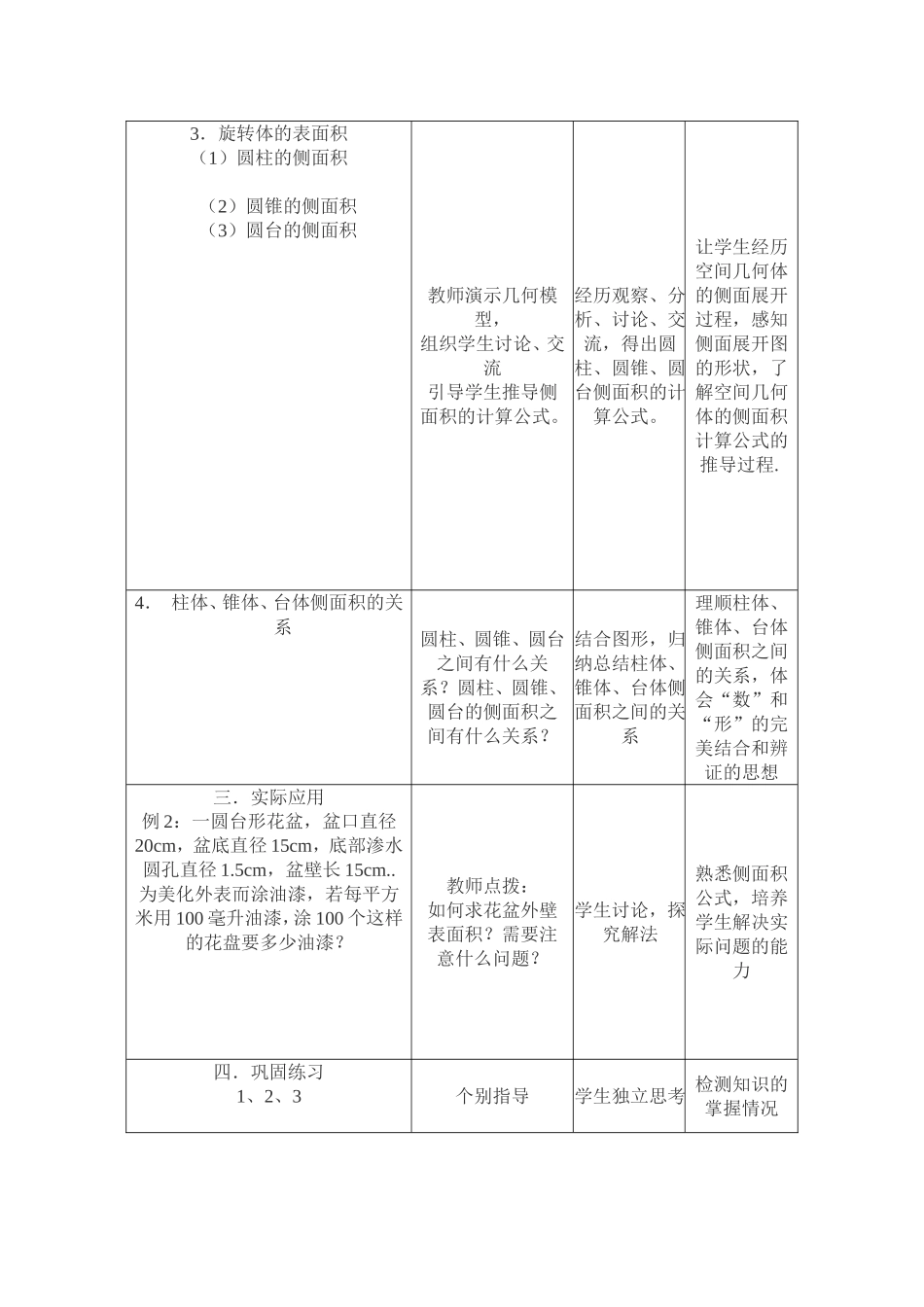
【教学设计】教学进程教师活动学生活动活动目标及说明一．温故知新多媒体展示前面学习过的一些多面体和旋转体，让学生分清哪些是多面体，哪些是旋转体，为本节课后面的学习打好基础
哪些是多面体，哪些是旋转体
如何计算棱柱、棱锥、棱台的表面积
回忆多面体、旋转体的定义，观察所给几何体并进行判断
通过提出新的问题，打破知识结构的平衡，引发学习的兴趣
二．探究新知1．多面体的表面积——棱柱、棱锥、棱台的表面积的计算方法结合多面体的结构特点，引导学生探求多面体表面积的求解方法
分析多面体的结构特点，思考求多面体表面积的方法
弄清多面体表面积的计算方法
2．典型例题例１:已知棱长为a，各面均为等边三角形的四面体S-ABC，求它的表面积
展示例题，引导学生分析问题，组织学生讨论、交流计算结果
分析问题，寻找解决问题的方法，交流、讨论
初步掌握多面体表面积的求法
3．旋转体的表面积（1）圆柱的侧面积（2）圆锥的侧面积（3）圆台的侧面积教师演示几何模型，组织学生讨论、交流引导学生推导侧面积的计算公式
经历观察、分析、讨论、交流，得出圆柱、圆锥、圆台侧面积的计算公式
让学生经历空间几何体的侧面展开过程，感知侧面展开图的形状，了解空间几何体的侧面积计算公式的推导过程
4．柱体、锥体、台体侧面积的关系圆柱、圆锥、圆台之间有什么关系
圆柱、圆锥、圆台的侧面积之间有什么关系
结合图形，归纳总结柱体、锥体、台体侧面积之间的关系理顺柱体、锥体、台体侧面积之间的关系，体会“数”和“形”的完美结合和辨证的思想三．实际应用例2：一圆台形花盆，盆口直径20cm，盆底直径15cm，底部渗水圆孔直径1
5cm，盆壁长15cm
为美化外表而涂油漆，若每平方米用100毫升油漆，涂100个这样的花盘要多少油漆
教师点拨：如何求花盆外壁表面积
需要注意什么问题
学生讨论，探究解法熟悉侧面积公式，培养学生解决实际问题的能力四．巩固练
