4.8正弦函数、余弦函数的图象和性质(四)VIP免费

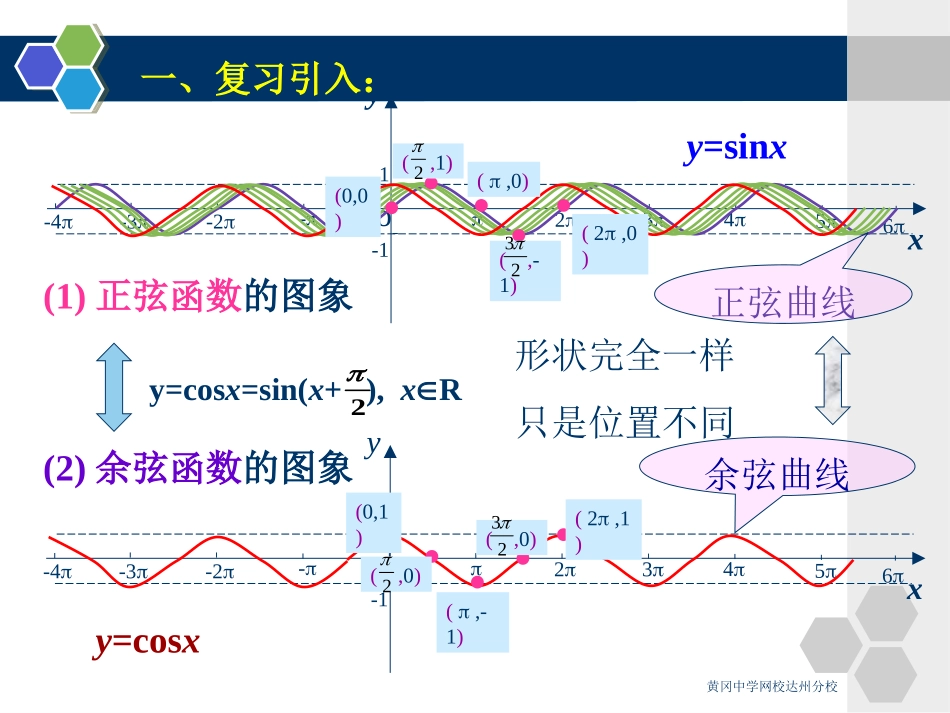
4.8正弦函数、余弦函数的图象和性质（四）2025年2月14日黄冈中学网校达州分校教学目标：1理解正、余弦函数的奇偶性、单调性的意义；2会判断简单函数的奇偶性、单调性和求单调区间；教学重点：简单函数的奇偶性、单调性和单调区间教学难点：复合函数的单调性和单调区间黄冈中学网校达州分校x6yo--12345-2-3-41(2)余弦函数的图象(1)正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同一、复习引入：(0,0)(,1)2(,0)(,-1)23(2,0)y=sinxy=cosx黄冈中学网校达州分校复习：1.y=sinx和y=cosx的图象黄冈中学网校达州分校正弦函数、余弦函数的图象与性质2.y=sinx和y=cosx的定义域和值域黄冈中学网校达州分校3.y=sinx和y=cosx的周期性黄冈中学网校达州分校正弦、余弦函数的图象和性质x6yo--12345-2-3-41y=sinx(xR)x6o--12345-2-3-41yy=cosx(xR)定义域值域周期性xRy[-1,1]T=2黄冈中学网校达州分校4.y=sinx和y=cosx的奇偶性黄冈中学网校达州分校sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数一般的,对于函数f(x)的定义域内的任意一个x，都有f(-x)＝-f(x)，则称f(x)为这一定义域内的奇函数。注意：若f(x)是奇函数，且x＝0在定义域内，则f(0)＝04.y=sinx和y=cosx的奇偶性奇函数的图象关于原点对称黄冈中学网校达州分校x6o--12345-2-3-41ycos(-x)=cosx(xR)y=cosx(xR)是偶函数一般的,对于函数f(x)的定义域内的任意一个x，都有f(-x)＝f(x)，则称f(x)为这一定义域内的偶函数。关于y轴对称偶函数的图象关于y轴对称黄冈中学网校达州分校sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数x6o--12345-2-3-41ycos(-x)=cosx(xR)y=cosx(xR)是偶函数定义域关于原点对称黄冈中学网校达州分校如何判断函数的奇偶性(1)判断函数的奇偶性时，应坚持“定义域优先”的原则，即先求函数的定义域，看其定义域是否关于原点对称．(2．)判断函数奇偶性的常用方法：①定义法：即从ƒ(-x)的解析式中拼凑出ƒ(x)的解析式，看[或]是否成立．②图象法：即作出y=ƒ(x)的图象，看其图象是否关于原点对称(或是否关于y轴对称)．)()(xfxf()()fxfx黄冈中学网校达州分校例1：判断下列函数的奇偶性：21(1)();|2|2xfxx[解析]2(1)10,11,xx2211()22xxfxxx)().()(xfxfxf为奇函数．20.x又定义域为[一1，1]，关于原点对称，(2)()cos(sin);fxx黄冈中学网校达州分校()cos[sin()]cos(sin)cos(sin)(),fxxxxfx∴ƒ(x)为偶函数．（2） xR,∈定义域关于原点对称黄冈中学网校达州分校例1：判断下列函数的奇偶性：1sincos1sincos(3)()1sincos1sincosxxxxfxxxxx2sin(sincos)2cos(sincos)222222(),2cos(sincos)2sin(sincos)222222xxxxxxfxxxxxxx解：0)2cos2(sin2cos2sinxxxx由可知kx2(),2xkkZ且即ƒ(x)定义域不关于原点对称，故ƒ(x)为非奇非偶函数．黄冈中学网校达州分校1)cos(sin2xxy例2．(08.全国Ⅰ文)是2A．最小正周期为的偶函数2B．最小正周期为的奇函数D．最小正周期为的奇函数C．最小正周期为的偶函数2(sincos)1sin2,yxxx,22T解析:因为所以有又正弦函数为奇函数，故选D．黄冈中学网校达州分校5.y=sinx和y=cosx的单调性黄冈中学网校达州分校y=sinx(xR)增区间为[，]其值从-1增至122xyo--1234-2-31223252722325xsinx2223…0………-1010-1减区间为[，]其值从1减至-1223[+2k,+2k],kZ22[+2k,+2k],kZ2231)y=sinx的单调性黄冈中学网校达州分校2)y=cosx的单调性y=cosx(xR)xcosx22-……0……-1010-1增区间为其值从-1增至1[+2k,2k],kZ减区间为，其值从1减至-1...