1.4.1正弦、余弦函数的图象4VIP免费

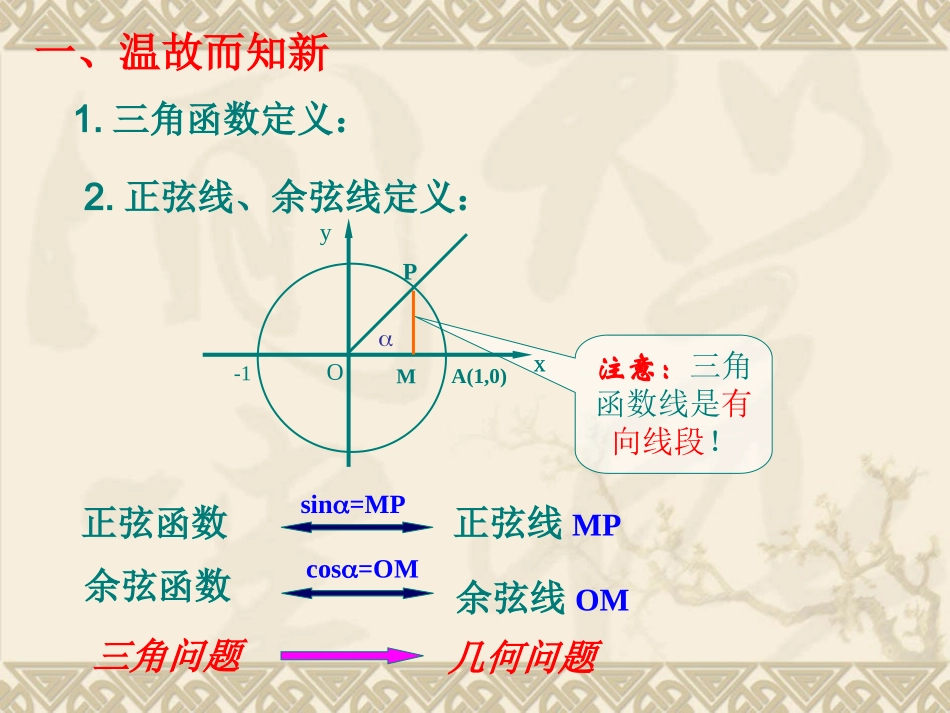
1.4.1正弦、余弦函数的图象X宜城二中：王冰涛注意：三角函数线是有向线段！正弦函数yxO-1PMA(1,0)sin=MPcos=OM正弦线MP余弦线OM一、温故而知新三角问题几何问题2.正弦线、余弦线定义：余弦函数1.三角函数定义：一、温故而知新：3.诱导公式：Sin(x+π/2)=Sin(2kπ+x)=cosxSinx(kz)∈规律：奇变偶不变，符号看象限。y=sinx(x[0,])21-1022322656723352yx●●●332346116633265●●●●●●●673435611●●●问题：1.如何作出正弦、余弦函数的图象？方法：利用单位圆中正弦线、余弦线作正、余弦函数的图象（几何法）(1)等分(2)作正弦线(3)平移(4)连线二、讲授新课：o1A问题2：由y=sinx（x[0,2]）的图像如何得到y=sinx（xR）的图像？x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322终边相同角的同名三角函数值相等。------由于cosx=Sin(x+π/2),所以余弦函数Rxxy,cos与函数Rxxy),2sin(问题3：如何由正弦函数图象得到余弦函数的图像？是同一个函数，余弦函数的图像可以通过正弦曲线向左平移π/2个单位长度而得到．x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线正弦曲线形状完全一样只是位置不同问题3：如何由正弦函数图象得到余弦函数的图像？简图作图步骤：(2)描点(定出五个关键点)；-oxy---11--132326567342335611262oxy---11--13232656734233561126与x轴的交点)0,0()0,()0,2(图象的最高点图象的最低点)1,(23与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,((五点作图法))1,2((1)列表(列出对图象形状起关键作用的五点)；(3)连线(用光滑的曲线顺次连结五个点)。问题4：什么是五点作图法？观察正、余弦函数在[0,2]上的图象，找出确定其形状的关键点。2223211xyo（2）列表例1用“五点法”作出下列函数的简图（1）y=sinx+1,x∈[0,2π];列表描点作图xxsin1sinx101010210102232（2）y=-cosx,x∈[0,2π].解:（1）]2,0[,sin1xxy]2,0[,sinxxyxxcosxcos02232211yo223x10-101-1010-1]2,0[,cosxxy]2,0[,cosxxy三、例题讲解2223211xyo三、练习：画出函数y=1-sinx,x[0,2π]∈的简图.列表描点作图xxsin1sinx101010012102232解法一:（五点法作图）1sin,[0,2]yxx]2,0[,sinxxy解法二:（变换法作图）①先作出函数y=sinx的图像；②其次将函数y=sinx的图像关于x轴对称得到y=-sinx的图像；③最后将函数y=-sinx的图像整体向上平移1个单位就是y=1-sinx的图像.正弦、余弦函数的图象正弦、余弦函数的图象小结1.正弦曲线、余弦曲线画法几何画法五点法图像变换2.正、余弦函数图象间的联系；yxo1-122322y=sinx，x[0,2]y=cosx，x[0,2]3.思想方法：数形结合的思想。1.作函数y=1+3cosx，x[0,2π]∈的简图。2.作函数y=-2sinx-1，x[0,2π]∈的简图。作业：再见