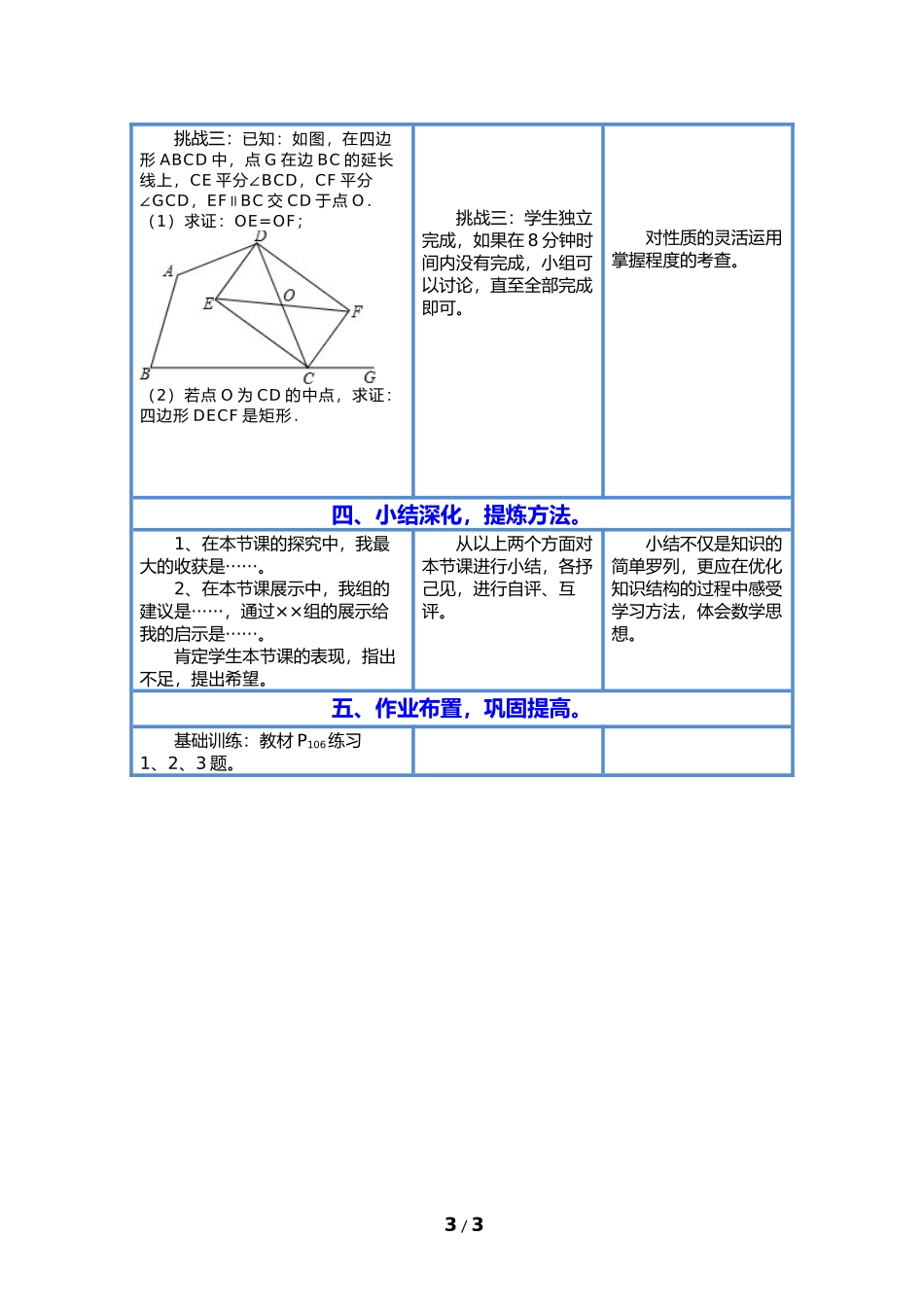
《矩形的判定》教学设计1/3教师行为学生学习活动设计意图一、创设情境,发现问题。1、问题:对于矩形,你了解多少?2、创设情景,引出课题。“小明为本班的进步明星做了一个相框,他找来长度相等的两根长木条作为长,两个相等的短木条作为宽,你能帮他检验一下现在的相框为矩形吗?”1、学生的积极性被调动起来,他们可能从矩形的面积、周长、性质等方面阐述自己对矩形的认识。2、肯定学生可以用定义判断相框是否为矩形的基础上,追问有无其它的方法,趁机引出课题,同时倡议班内同学都应该为班集体出力。1、从学生已有的认知出发,既复习了旧知识,又使课堂气氛活跃起来,使学生在进入新课之前其情感和态度都达到最佳。2、从学生身边的问题抽象出数学问题,体现了数学来源于生活又服务于生活的道理,二、尝试探索,解决问题。1、出示问题,引发猜想①、你猜想判断相框是否为矩形的方法有哪些?②、你为什么有这样的猜想?③你能否证明猜想的正确性?教师出示以上问题后,鼓励学生先独立思考,猜想判断矩形的方法,小组交流形成共识后,将自己的猜想板演到黑板上。2、鼓励尝试,验证猜想①、继续鼓励学生以独立思考、小组交流、全班展示的方式展开探究,以合作者、参与者的身份指导学生用各种方法证明猜想。②、教师与学生一起倾听各小组不同观点,师生共同查缺补漏,对于猜想不恰当或验证方法有误的小组,引导学生通过举反例或逻辑推理的方法反驳对方,使其明白错误的原因,加深认识。最后,师生达成共识:1、学生经过独立思考、小组交流,互相补充后,在小组形成一致意见的情况下,派代表将本小组的猜想板演到黑板上。学生可能有如下猜想:①、对角线相等的四边形是矩形。或对角线相等的平行四边形是矩形或对角线互相平分且相等的四边形是矩形。②、四个角(三个角)是直角的四边形是矩形。学生经过独立思考、小组交流后各组选代表上台验证本组的猜想。对于猜想①一部分学生可能受教材的启示,用两条相等的绳子将它的中点作为对角线的交点,确定一个平行四边形,再测量一个角1、通过教师设置的三个问题鼓励学生当面临着一道很难解决的问题时,可以从已有的经验出发做出猜想。学生形形色色的猜想给他们不同的感受,在锻炼学生语言表达能力的同时也为下一步的探究指明了方向。独立思考给每个同学思考的权利,小组交流,交流方法,互通有无,全班展示,达成共识,形成自信。在整个探究的过程中,教师将课堂和时间最大限度的还给了学生给学生创造出一个自由发展的舞台,在这个过程中,学2/3①、对角线相等的平行四边形是矩形。②、三个角是直角的四边形是矩形。是否为90°来验证,当然也有同学会先画一个平行四边形再测量角的度数,还有一部分同学可能用全等的知识进行逻辑证明得出矩形的判定方法。对于猜想②估计大部分同学会用逻辑推理的方法去证明,也有的同学会通过测量两组对边是否相等,确定是否为平行四边形后,然后根据定义来确定。生感受到的不仅是知识的结论,更多是在探索、展示过程中的经历和经历中所蕴含的思想方法。三、引导落实,应用提高鼓励学生完成习题训练,挑战自我。小明在判断相框是否为矩形的过程中,能否以下列方法作为依据,为什么?挑战一:⑴有一个角是直角的四边形是矩形;()⑵有四个角是直角的四边形是矩形;()⑶四个角都相等的四边形是矩形()⑷对角线相等的四边形是矩形;()⑸对角线互相平分且相等的四边形是矩形;()⑹两组对边分别平行,且对角线相等的四边形是矩形。()挑战二:小明用长度相等的两个长木条和长度相等的短木条做如图所示的相框后,下面是他经过测量,计算相框面积的过程,你认为他的解法正确吗?正确吗?SABCDABCD=AB∙BC=6ⅹ8=488=48挑战一:学生很容易利用本节课的内容解决以上问题,在回答过程中须阐明理由。不足之处小组内同学互相补充。挑战二:此题结合图形,学生很容易形成错觉,让学生在自己诊断的基础上进行会诊,在这个过程中诊断出错的学生必会恍然大悟,为以后此类问题的解决敲响了警钟,规范了学生的解题格式。使学生灵活的运用矩形的三种判定方法,做到举一反三、触类旁通。错误是很好的教育资源,针对本节课学生易错点...