第5课时、圆周角（1）VIP免费

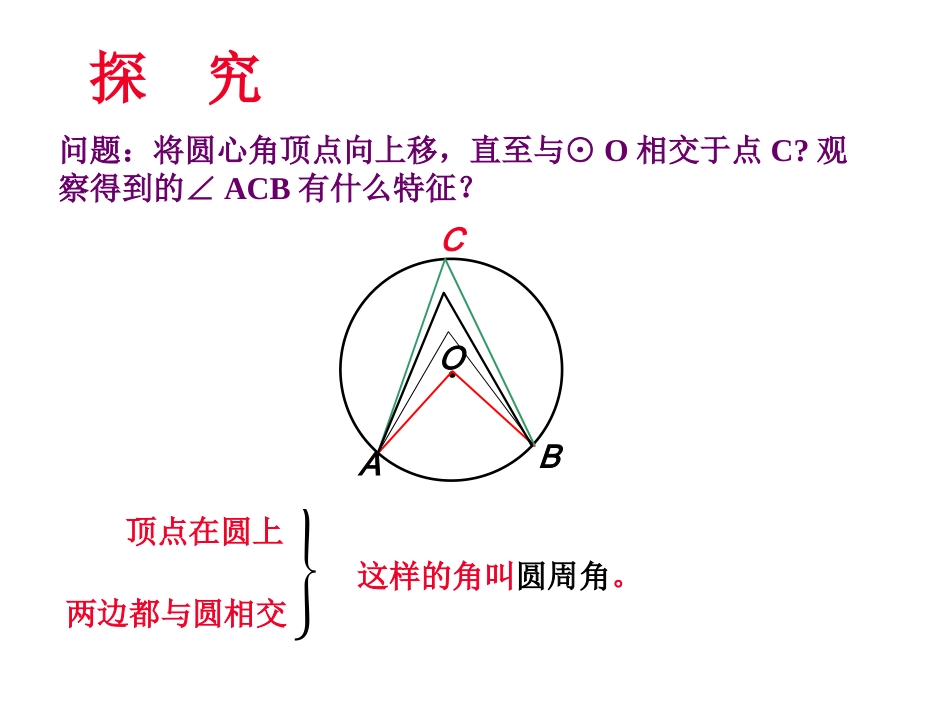
圆周角(1)学科网回忆1.什么叫圆心角?.OAB顶点在圆心的角叫圆心角2.圆心角、弧、弦三个量之间关系的一个结论，这个结论是什么？在同圆（或等圆）中，如果圆心角、弧、弦有一组量相等，那么它们所对应的其余两个量都分别相等。探究.OA问题：将圆心角顶点向上移，直至与⊙O相交于点C?观察得到的∠ACB有什么特征？C顶点在圆上两边都与圆相交这样的角叫圆周角。B.OBCA问题：圆周角概念与圆心角概念在表述上有什么区别？答：圆周角强调角的两边与圆相交，而圆心角不必强调这一点。因为以圆心为顶点的角一定会和圆相交。问题探讨：判断下列图形中所画的∠P是否为圆周角？并说明理由。PPPP不是是不是不是顶点不在圆上。顶点在圆上，两边和圆相交。两边不和圆相交。有一边和圆不相交。ABCO1、有没有圆周角？2、有没有圆心角？3、它们有什么共同的特点？它们都对着同一条弧⌒⌒⌒⌒4、同一条弧所对的圆心角和圆周角个有几个？学科网下列图形中，哪些图形中的圆心角∠BOC和圆周角∠A是同对一条弧。ABCOABCOABCOABCODABCOD(1)(1)(2)(2)(3)(3)(4)(4)(5)(5)√√√•如图,观察圆周角∠ABC与圆心角∠AOC,它们的大小有什么关系?●OABC●OABC●OABC猜测：一条弧所对的圆周角等于这条弧所对的圆心角的度数的一半。分情况讨论的思想方法分情况讨论的思想方法在圆上任取一个圆周角，观察圆心与圆周角的位置关系有几种情况？教师提示:注意圆心与圆周角的位置关系.（1）圆心是圆周角的一条边上，（2）圆心在圆周角的内部，（3）圆心在圆周角的外部．1.第一种情况：ABCO OA=OC∴∠A=C∠又∠BOC=A∠＋∠C∴∠BOC=2A∠∠即A=BOC∠21圆周角∠BAC与圆心角∠BOC的大小关系.老师期望:你可要理解并掌握这个模型.ABCOD证明：由第1种情况得∠即BAC=BOC∠21∠BAD＝∠BOD21∠CAD＝∠COD21∠BAD＋∠CAD＝∠BOD＋∠COD21212.第二种情况：老师提示:能否转化为1的情况?证明：作射线AO交⊙O于D。由第1种情况得∠即BAC=BOC∠21∠BAD＝∠BOD21∠CAD＝∠COD21∠CAD－∠BAD＝∠COD－∠BOD2121ABCOD3.第三种情况：老师提示:能否转化为1的情况?•综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是:•同弧所对的圆周角等于它所对的圆心角的一半.●OABC●OABC●OABC即∠ABC=∠AOC.21归纳总结在同圆或等圆中，同弧(或等弧）所对的圆周角相等；都等于这条弧所对的圆心角的一半．圆周角定理·ABCDEO思考:在同圆或等圆中，相等的圆周角所对的弧相等吗?ABOC如图,AB是直径,则∠ACB=＿＿＿＿90度半圆（或直径）所对的圆周角是直角，90度的圆周角所对的弦是直径。·ABC1OC2C3一条弧所对的圆周角等于它所对的圆心角的一半．圆周角定理直径（或半圆）所对的圆周角是直角，90°的圆周角所对的弦是直径．推论·ABCDEO同弧或等弧所对的圆周角相等．推论1、如图，在⊙O中，ABC=50°，则∠AOC等于（）A、50°；B、80°；C、90°；D、100°ACBOD2、如图，△ABC是等边三角形，动点P在圆周的劣弧AB上，且不与A、B重合，则∠BPC等于（）A、30°；B、60°；C、90°；D、45°CABPB练习练习::3、求圆中角X的度数OO练习练习::AX120°B（1）（2）.600P1200BA.70°x350学科网4.试找出下图中所有相等的圆周角.ABCD12345678∠2=∠7∠1=∠4∠3=∠6∠5=∠85、如图，△ABC的顶点A、B、C都在⊙O上，∠C＝30°，AB＝2，则⊙O的半径是。CABO解：连接OA、OB ∠C=30°，∴∠AOB=60°又 OA=OB，∴△AOB是等边三角形∴OA=OB=AB=2，即半径为2。26：已知⊙O中弦AB的等于半径，求弦AB所对的圆心角和圆周角的度数。OAB圆心角为60度圆周角为30度或150度。在同圆或等圆中，如果两个圆周角相等，它们所对弧一定相等吗？为什么？在同圆或等圆中，如果两个圆周角相等，它们所对的弧一定相等．ABCD在同圆或等圆中相等的圆周角所对的弧相等.则∠D=A∠∴ABCD∥如图,若AC=BD⌒⌒例1、如图，⊙O直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC、AD、BD的长．86102222ACABBC又在Rt△ABD中，AD2+BD2=AB2，221052(cm)22ADBDAB·ABCDO解： AB是直径，∴∠ACB=∠ADB=90°．在Rt△ABC中， CD平分∠ACB，∴AD=BD.106））AD=BD⌒⌒⌒⌒∴·2、求证：如果...