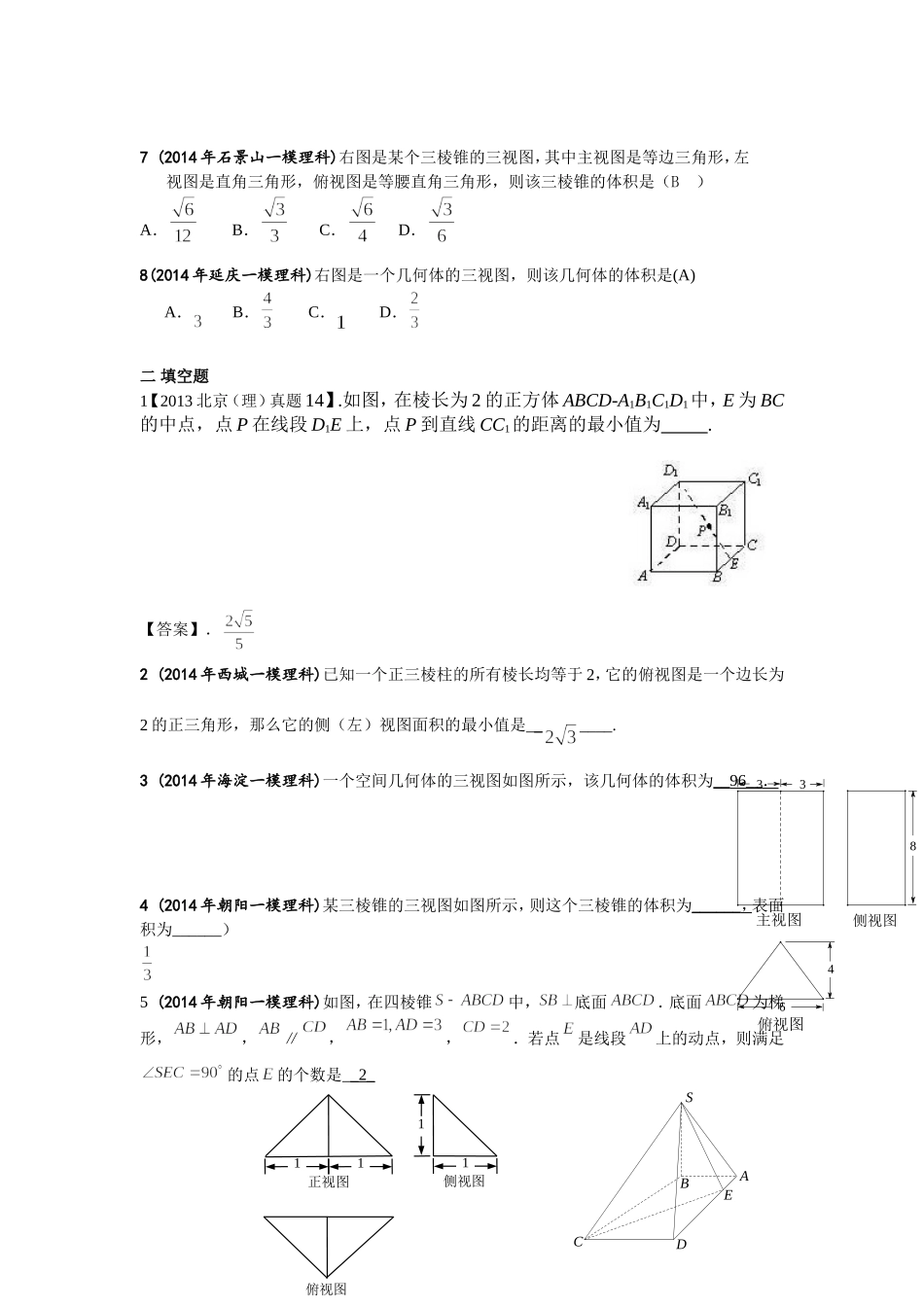
立体几何一选择题1【2014北京(理)真题8】如图,正方体ABCD—A1B1C1D1的棱长为2,动点E,F在棱A1B1上,动点P,Q分别在棱AD,CD上.若EF=1,A1E=x,DQ=y,DP=z(x,y,z大于零),则四面体P—EFQ的体积()A.与x,y,z都有关B.与x有关,与y,z无关C.与y有关,与x,z无关D.与z有关,与x,y无关【答案】D2【2014北京(理)真题7】在空间直角坐标系中,已知.若分别是三棱锥在坐标平面上的正投影图形的面积,则()A.B.且C.且D.且【答案】D3【2012北京(理)真题7】某三棱锥的三视图如图所示,该三棱锥的表面积是(A)(B)(C)(D)俯视图侧(左)视图正(主)视图4324【答案】.B4【2011北京(理)真题7】某四面体三视图如图所示,该四面体四个面的面积中最大的是()[来源:学_科_网]A.B.C.D.【答案】C5(2014年西城一模理科)如图,设为正四面体表面(含棱)上与顶点不重合的一点,由点P到四个顶点的距离组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有(C)(A)4个(B)6个(C)10个(D)14个6(2014年丰台一模理科)棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是(B)(A)143(B)4(C)103(D)3侧视图俯视图主视图2211111主视图左视图俯视图7(2014年石景山一模理科)右图是某个三棱锥的三视图,其中主视图是等边三角形,左视图是直角三角形,俯视图是等腰直角三角形,则该三棱锥的体积是(B)A.B.C.D.8(2014年延庆一模理科)右图是一个几何体的三视图,则该几何体的体积是(A)A.B.C.D.二填空题1【2013北京(理)真题14】.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为.【答案】.2(2014年西城一模理科)已知一个正三棱柱的所有棱长均等于2,它的俯视图是一个边长为2的正三角形,那么它的侧(左)视图面积的最小值是______.3(2014年海淀一模理科)一个空间几何体的三视图如图所示,该几何体的体积为__96__.4(2014年朝阳一模理科)某三棱锥的三视图如图所示,则这个三棱锥的体积为______,表面积为______)5(2014年朝阳一模理科)如图,在四棱锥中,底面.底面为梯形,,∥,,.若点是线段上的动点,则满足的点的个数是__2_1正视图侧视图俯视图111BCDESA33846俯视图主视图侧视图三解答题1【2014北京(理)真题17】.(本小题14分)如图,正方形的边长为2,分别为的中点,在五棱锥中,为棱的中点,平面与棱分别交于点.(1)求证:;(2)若底面,且,求直线与平面所成角的大小,并求线段的长.MPHGFEDCBA(1)【答案】.证明:(2)如图建立空间坐标系,各点坐标如下:设的法向量为,,,即,令得:又,直线与平面所成角为设,由则又,,,2【2013北京(理)真题17】.(本小题共14分)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(Ⅰ)求证:AA1⊥平面ABC;(Ⅱ)求二面角A1-BC1-B1的余弦值;(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值.【答案】.解:(Ⅰ)因为,所以.因为,且AA1垂直于这两个平面的交线AC,xzy所以⊥平面.(Ⅱ)由(Ⅰ)知,⊥.由题知AB=3,BC=5,AC=4,所以.如图,以A为原点建立空间直角坐标系,则,,,.设平面的法向量为,则即令z=3,则x=0,y=4,所以.同理可得平面的法向量为.所以由题知二面角为锐角,所以二面角的余弦值为(Ⅲ)设点D是直线BC1上一点,且所以.解得所以由,即,解得.因为,所以在线段BC1上存在点D,使得.此时3【2012北京(理)真题16】(本小题共14分)如图,在中,,,,、分别为、上的点,C1B1A1CBAD图1图2ADECBA1MDECB且//,,将沿折起到的位置,使,如图.(Ⅰ)求证:平面;(Ⅱ)若是的中点,求与平面所成角的大小;(Ⅲ)线段上是否存在点,使平面与平面垂直?说明理由.【答案】.解:(1),平面,又平面,又,平面(2)如图建系,则,,,∴,设平面法向量为则∴∴∴又 ∴∴∴与平面所成角的大小(3)设线段上存在点,设点坐标为,则则,设平面法向量为则∴∴假设平面与平面垂直则,zyxA1(0,0,23)D(-2,0,0)E(-2,2,0)B(0,3,0)C(0,0...