高中数学 3-2-3 立体几何中的向量方法 空间向量与垂直关系课件 新人教A版选修2-1 课件VIP免费

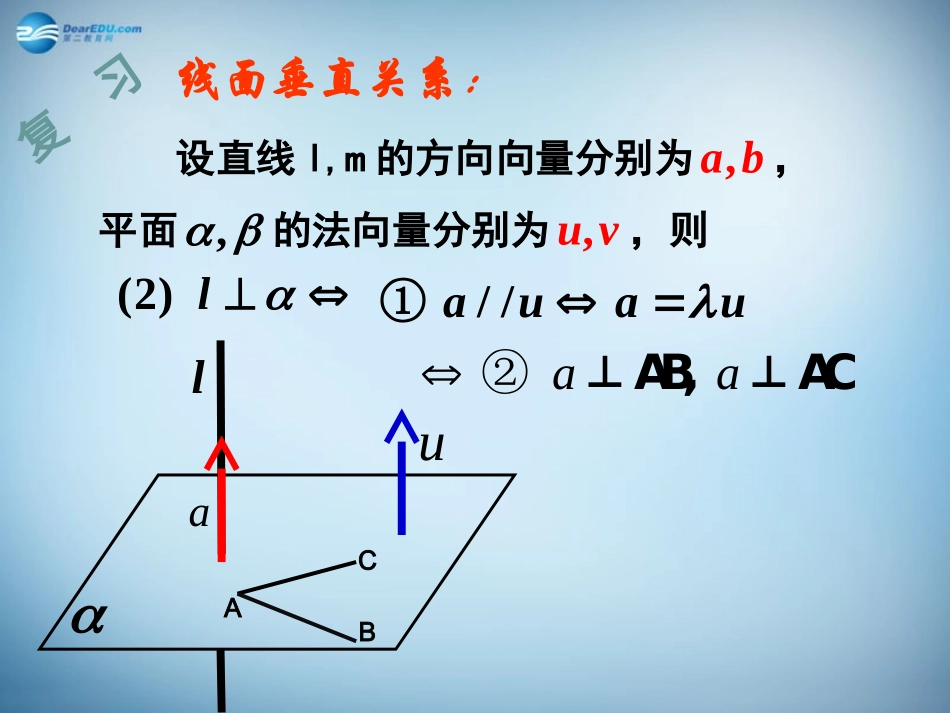
3.2.3立体几何中的向量方法——空间向量与垂直关系(1)lm0abab线线垂直关系：设直线l,m的方向向量分别为,ab，平面,的法向量分别为,uv，则lmab复习线面垂直关系：设直线l,m的方向向量分别为,ab，平面,的法向量分别为,uv，则(2)l//auau①lauABCaa��②⊥AB,⊥AC复习面面垂直关系：设直线l,m的方向向量分别为,ab，平面,的法向量分别为,uv，则3（）0uvuvαβuv复习1．若平面α、β的法向量分别为a＝(－1,2,4)，b＝(x，－1，－2)，并且α⊥β，则x的值为()A．10B．－10C.12D．－122．若直线l的方向向量为＝(－1,0，－2)，平面α的法向量为＝(4,0,8)，则(A．l∥αB．l⊥αC．l⊂αD．l与α斜交BBau例：如图所示，在正方体ABCD－A1B1C1D1中，O为AC与BD的交点，G为CC1的中点.求证：1;AOBG（1）1.ABDGBD（3）平面平面1;AOGBD（2）平面11111a,b,cABADAA�设，ab=0,ac=0,bc=0.则11�而AO=AA+AO1();2cabBGBCCG�1b;2c1111()(b)222AOBGcabc�11111bbbcc22244cabccab11,AOBGAOBG�证明：（1）证法一：abc向量法=011()2ABAD�=AA+11+2BCAA�例：如图所示，在正方体ABCD－A1B1C1D1中，O为AC与BD的交点，G为CC1的中点.求证：1;AOBG（1）1.ABDGBD（3）平面平面1;AOGBD（2）平面1;AOBG（1）11111a,b,cABADAA�设，ab=0,ac=0,bc=0.则11�而AO=AA+AO1();2cabBDADAB�b;a111()(b)22AOBDcaba�1111bbba2222cabcaaab111,,,AOBGBGGBDBDGBDBGBDBAOBDAOGBD����又平面面平面平证明：（2）证法一:(向量法)abc=011()2ABAD�=AA+例：如图所示，在正方体ABCD－A1B1C1D1中，O为AC与BD的交点，G为CC1的中点.求证：1.ABDGBD（3）平面平面1;AOBG（1）1;AOGBD（2）平面1;AOGBD（2）平面1D�那么（1O,0,0），B(2，2，0),A(2，0，2),G(0，2，1)DB=(2，2，0),DA=(2，0，2)，GB=(2，0，-1),如图，取D为坐标原点，分别以DA、DC、DD1所在的直线为x轴，y轴，z轴建立空间直角坐标系．证明：（3）1111111111111111(,,),=0+=0=1=-1z=-1+=0=(1,1,1)0ABDnxyznDBxyxyxznDnA����设平面的法向量为则，取，则，，22222222222222222122121(,,),=0+y=0=-y2=02==0=1=-12=1+1-2=(1,1,2)0GBDnxyznDBxxxzxznGBxyznnnnABnDGBD������设平面的法向量为则取，则，，则，即平面平面xZY在直三棱柱ABC－A1B1C1中，AB⊥BC，AB＝BC＝2，BB1＝1，E为BB1的中点。求证：平面AEC1⊥平面A1AB1BC1CEA1AB1BC1CEXY�1111A（2,0,0），C(0，2，0),E(0，0，),C(0，2，1)21AC=(-2，2，0),CC=(0，0，1)，AE=(-2，0，)，AC=(-2，2，1)2如图，取B为坐标原点，分别以BA、BC、BB1所在的直线为x轴，y轴，z轴建立空间直角坐标系．证明:111111111111111(,,),=0-+=0=1=1=0=(1,100,)AACCnxyznACxyxyznCnC����设平面的法向量为则，取，则，122222222122222212121211(1(,,),1=0-2+=02=022=0=1=-14=1,1,41)-=0AECnxyznAExznACxyzxyznnnnAEnCAACC�����设平面的法向量为则取，则，，则，即平面平面Z•作业：P112A组第2题（坐标法）第3题（向量法）