高中数学 422常见曲线物极坐标方程(1)学案 苏教版选修4-2 课件VIP免费

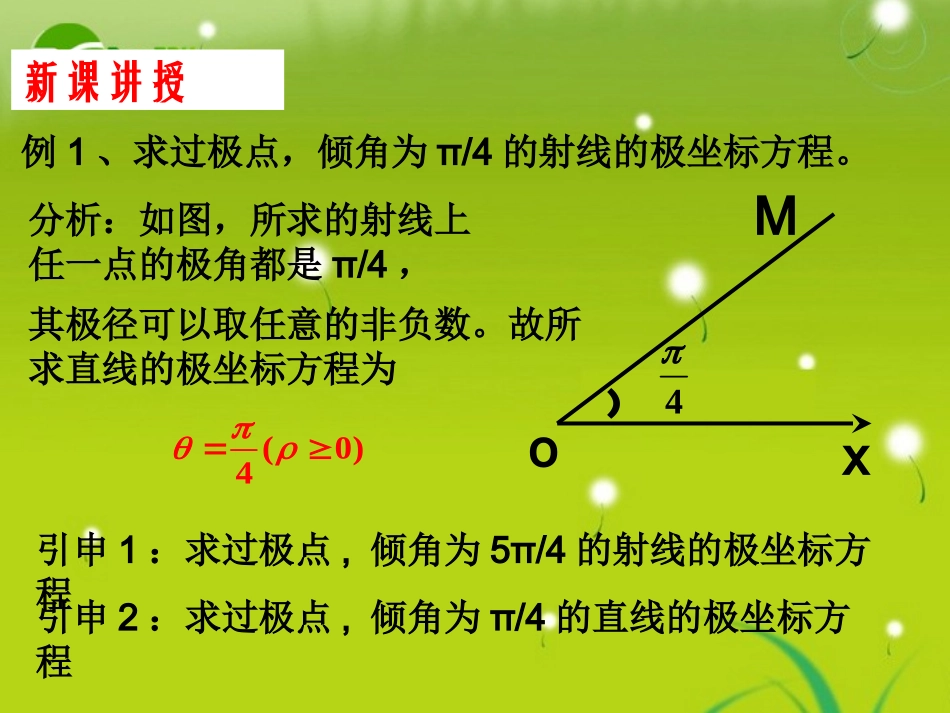
常用曲线的极坐标方程----直线的极坐标方程新课引入思考1：在平面直角坐标系中1、过点(3,0)且与x轴垂直的直线方程为____;过点(3,3)且与x轴垂直的直线方程为______x=3x=32、过点(a,b)且垂直于x轴的直线方程为____x=a特点：所有点的横坐标都是一样，纵坐标可以取任意值。与直角坐标系里的情况一样，求曲线的极坐标方程就是找出曲线上动点Ｐ的坐标与之间的关系，然后列出方程f(,)=0，再化简并讨论。思考2:怎样求曲线的极坐标方程？例1、求过极点，倾角为π/4的射线的极坐标方程。oMx﹚4分析：如图，所求的射线上任一点的极角都是π/4，其极径可以取任意的非负数。故所求直线的极坐标方程为(0)4新课讲授引申1：求过极点,倾角为5π/4的射线的极坐标方程引申2：求过极点,倾角为π/4的直线的极坐标方程和前面的直角坐标系里直线方程的表示形式比较起来，极坐标系里的直线表示起来很不方便，要用两条射线组合而成。原因在哪？为了弥补这个不足，可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为()4R或5()4R原因在ρ≥0例2设点P的极坐标为(ρ0,θ0,)，直线l过点P且与极轴所成的角为,求直线l的极坐标方程。oxMP﹚﹚00解：如图，设点M(ρ,θ)为直线上除点P外的任意一点，连接OM，在△MOP中有显然点P的坐标也是它的解。00sin()sin()00sin()sin()OPsinsinOMOMPOPM00sin()sin()00上式是过（，），倾斜角为的直线的极坐标方程.010ll、当直线过极点，即＝时，直线的方程是什么？2M(,)2lb、当直线过点且平行于极轴时，直线的极坐标方程是什么？练习1：sinb3、求过点A(a,0)(a>0)，且垂直于极轴的直线l的极坐标方程。ox﹚AM求直线的极坐标方程步骤:1、根据题意画出草图；2、设点M(ρ,θ)是直线上任意一点；3、连接MO；4、根据几何条件建立关于ρ,θ的方程，并化简；5、检验并确认所得的方程即为所求。4、设点A的极坐标为(a,0)，直线l过点A且与极轴所成的角为α,求直线l的极坐标方程。解：如图，设点M(ρ,θ),为直线l上异于A的点,连接OM，在△MOA中有﹚oMxAsin()sin()a即sin()sina显然A点也满足上方程.练习2：按下列条件写出直线的极坐标方程：(1)A(6)(2)B(5)(3)C(8)62(4)D(23,0)3经过极点和点，的直线；5经过点，，且垂直于极轴的直线；经过点，，且平行于极轴的直线；经过点，且倾斜角为的直线；(1)5(2)cos5(3)sin42(4)sin()33小结：直线的几种极坐标方程。1、过极点2、过某个定点，且垂直于极轴3、过某个定点，且与极轴成一定的角度