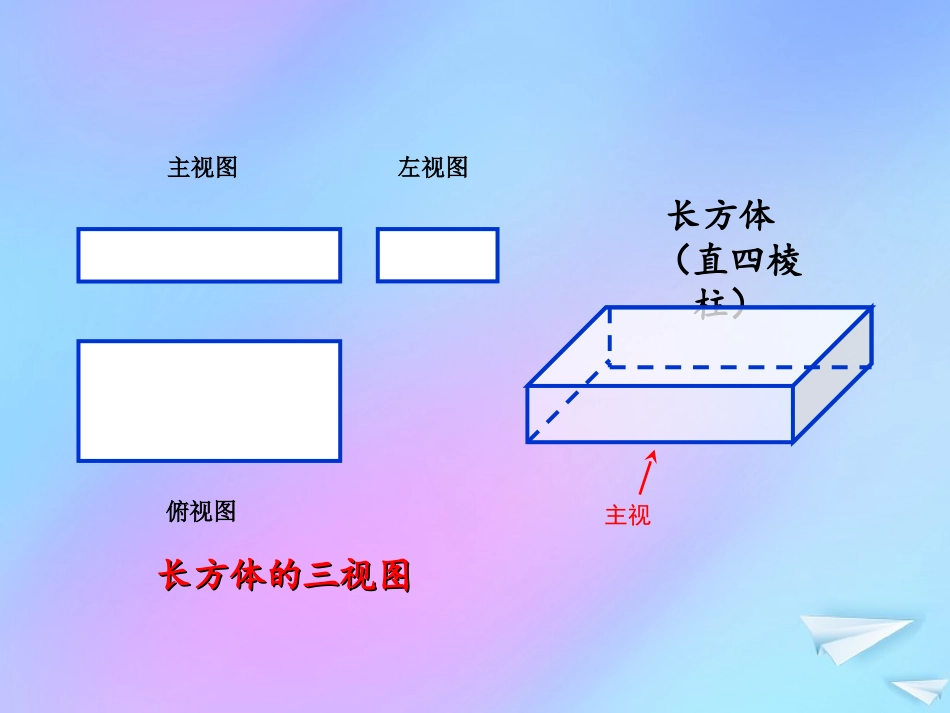
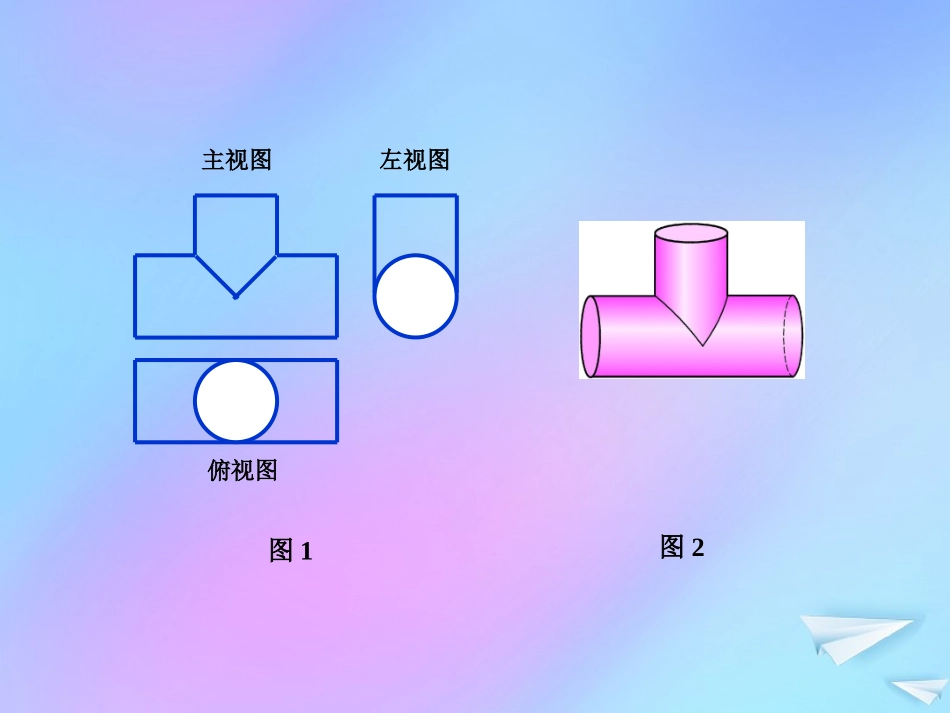
主视图长方体的三视图长方体的三视图左视图俯视图长方体(直四棱柱)主视你认识它吗?三通接头图2图1左视图主视图俯视图§3.2由三视图还原成实物图主视图左视图俯视图一、说一说球体主视主视图左视图俯视图一、说一说圆柱主视主视图左视图俯视图一、说一说圆锥主视主视图左视图俯视图一、说一说圆台主视主视图左视图俯视图球体主视主视图左视图俯视图圆柱主视主视图左视图俯视图圆锥主视主视图左视图俯视图圆台主视一、说一说主视图左视图俯视图一、说一说长方体(直四棱柱)主视一、说一说俯视图主视图左视图正六棱柱主视俯视图主视图左视图一、说一说正四棱锥主视主视图俯视图左视图一、说一说正四棱台主视一、说一说主视图左视图俯视图四棱柱(长方体)主视主视图左视图俯视图正四棱锥主视主视图俯视图左视图正四棱台主视俯视图主视图左视图正六棱柱主视一、说一说1.若视图是圆,则该几何体很可能是旋转体;若视图是多边形,则该几何体很可能是多面体。2.若视图是矩形,则该几何体很可能是柱体;若视图是三角形,则该几何体很可能是锥体;若视图是梯形,则该几何体很可能是台体。简单几何体还原成实物图的方法:俯视图主视图左视图正五棱锥主视一、说一说左视图主视图俯视图三棱柱主视俯视图主视图左视图二、想一想简单组合体主视二、想一想主视图左视图俯视图主视三棱柱二、想一想主视图左视图俯视图主视四棱柱1.将每个视图转化(分解或补全)为基本图形(圆、矩形、三角形、梯形等)。2.结合对应部分的三视图想象对应的基本几何体。3.结合虚实线,概括组合体。4.对照检查三视图和实物图是否相符。二、想一想简单组合体还原成实物图的方法:三、摆一摆俯视图左视图主视图(1)主视图左视图俯视图(2)主视图左视图(4)俯视图俯视图(3)主视图左视图三、摆一摆主视俯视图左视图主视图三、摆一摆左视图主视图俯视图主视三、摆一摆主视图俯视图左视图主视三、摆一摆主视图左视图俯视图主视五、画一画根据三视图想象物体原形,并画出物体的实物草图。俯视图主视图左视图(1)左视图俯视图主视图(2)五、画一画俯视图主视图左视图(1)主视主视(2)左视图俯视图主视图六、算一算主视13VShSh锥体棱锥和圆锥的体积公式:,其中,为锥体的底面积,为锥体的高。2344,,3SRVRR球面球球的表面积和体积公式:其中,为球的半径。1.某几何体的三视图如图1所示,则其表面积为()。图1俯视图主视图21左视图22.某几何体的三视图如图2所示,则其体积为()。【2013年陕西高考文科第12题】【2013年陕西高考理科第12题】图2俯视图左视图11主视图1233主视俯视图左视图22主视图24.某几何体的三视图如图4所示,则其体积为()。【2011年陕西高考理、文科第5题】图43.下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()。(补充)13VShSh锥体棱锥和圆锥的体积公式:,其中,为锥体的底面积,为锥体的高。2344,,3SRVRR球面球球的表面积和体积公式:其中,为球的半径。283图34443223)D(28)C(24)B(20)A(C【2016年全国Ⅱ卷高考理科第6题,文科第7题】六、算一算总结几何体还原高博视图为圆旋转体,多边围棱多面体。矩形思柱三角锥,看见梯形就想台。组合体还原高博视图转化分解补,努力想象基本体。虚实概括相结合,对照检查组合体。1.必做题:课本第20页,A组,第7题。2.选做题:课本第55页,B组,第2题。3.思考交流题:右图是一个奖杯的三视图,请画出它的实物图,并与同伴交流。(课本第18页图1-37)课后作业左视图主视图俯视图谢谢!