高中数学 第一章 立体几何初步 17 柱、锥、台的侧面展开与面积课件 北师大版必修2 课件VIP免费

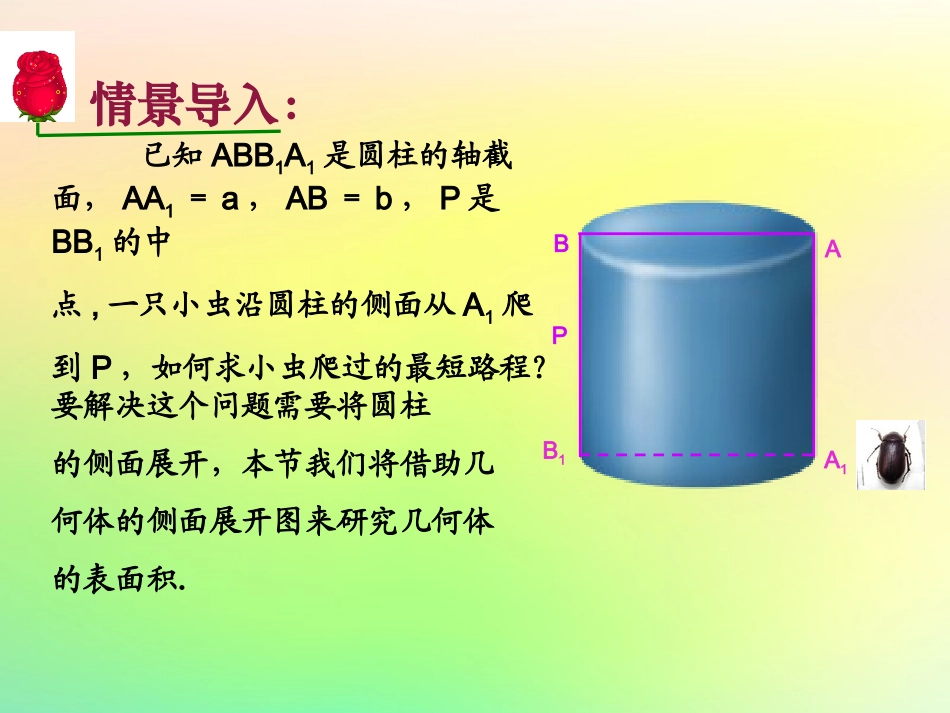
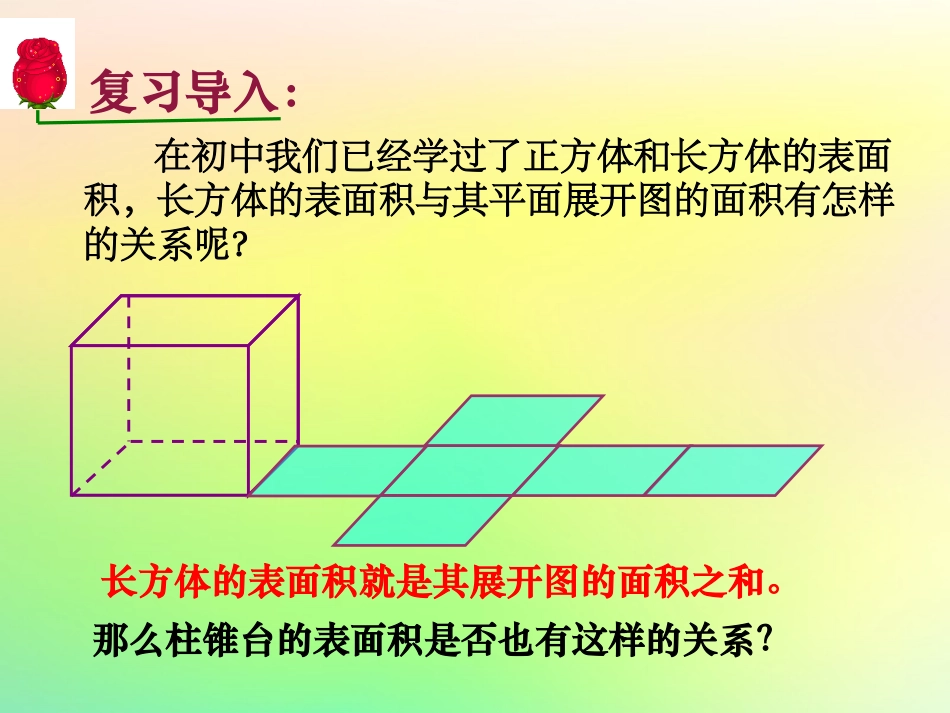
已知ABB1A1是圆柱的轴截面，AA1＝a，AB＝b，P是BB1的中点,一只小虫沿圆柱的侧面从A1爬到P，如何求小虫爬过的最短路程？要解决这个问题需要将圆柱的侧面展开，本节我们将借助几何体的侧面展开图来研究几何体的表面积．情景导入：A1B1BAP在初中我们已经学过了正方体和长方体的表面积，长方体的表面积与其平面展开图的面积有怎样的关系呢？复习导入：长方体的表面积就是其展开图的面积之和。那么柱锥台的表面积是否也有这样的关系？思考1:把圆柱的侧面沿着一条母线展开，得到什么图形?展开图与原图有什么关系？长方形的面积等于圆柱的侧面积探究点1.圆柱、圆锥、圆台的侧面积问题探究长方形宽＝l将空间问题平面化，是解决立体几何问题最基本的方法.方法规律:lr长方形长=2r==2SSrl圆柱侧长方形思考2:把圆锥的侧面沿着一条母线展开，得到什么图形?展开的图形与原图有什么关系？扇形SS圆锥侧扇＝转化rlnlC2r180扇Rl扇＝扇形SS圆锥侧扇＝23601802nlnllrlnS圆锥侧＝rl思考3:把圆台的侧面沿着一条母线展开，得到什么图形?展开的图形与原图有什么关系？扇环SS圆台侧扇环＝转化因为即121,rlxrr所以SSS扇环大扇小扇21221rlxrxrlrrx（）2112).rlrlrrl（在S0A和S0B中，SABxl扇环22rp12rp2r1ro′12)SSrrl环圆台侧扇＝（分析：抓住轴截面三角形的相似比是解题的关键.思考4：将圆柱、圆锥、圆台的侧面积公式进行比较，你能发现它们的联系和区别吗？Srl圆锥侧12Srrl圆台侧10r=2Srl圆柱侧12rrr==例1.一个圆柱形的锅炉，底面直径,高，求锅炉的表面积（保留2个有效数字）.1dm2.3hm解：22SS2S=2()2112.328.8.4ddhm侧面积底面积答：锅炉的表面积约为28.8m.分析：圆柱表面积与侧面积的关系.答：圆台的侧面积为600cm2.例2圆台的上、下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°，那么圆台的侧面积是多少？（结果中保留）12(rr)AB解:如图，设上底面周长为c,因为扇环的圆心角是180°，所以c=·SA又因为c=2×10=20,所以SA=20.同理SB=40.所以，AB=SB-SA=20,S圆台侧=2(1020)20600().cm·12(rr)AB思考1：把直棱柱、正棱锥、正棱台的侧面分别沿着一条侧棱展开，分别得到什么图形？侧面积是多少？探究点2.直棱柱、正棱锥、正棱台的侧面积类比圆柱、圆锥、圆台！chSch直棱柱侧其中为底面周长，为高1Sch'2正棱锥侧＝ch其中为底面周长，为斜高，即侧面等腰三角形的高.h′1Scc')h'2正棱台侧＝（c,ch其中分别为上、下底面周长,为斜高，即侧面等腰梯形的高.h′思考2：将直棱柱、正棱锥、正棱台的侧面积公式进行比较,你能发现它们的联系和区别吗？1cc')'2Sh正棱台侧＝（＋1'2Sch正棱锥侧＝'Schch直棱柱侧＝=c'0=c'c=思考3：柱、锥、台的侧面积公式之间有什么关系？提示：柱和锥都可以看作是由台体变化而成的几何体.柱可以看作是上下底面全等的台体，锥可以看作是上底面缩小成一个点的台体.观察它们的侧面积公式不难发现：柱和锥的侧面积公式都可以看作是由台体的侧面积公式演变而来的.1.将边长为1的正方形以其一边所在的直线为旋转轴旋转一周,所得几何体的侧面积是()A.4πB.8πC.2πD.π2.圆锥底面半径为6,高是6，中截面把圆锥截成一个小圆锥和一个圆台，则圆台的侧面积为______.C2723.某几何体的三视图如图所示,该几何体的表面积是_____.【解析】由三视图可知,原几何体是一个底面是直角梯形,高为4的直四棱柱,其底面积为28,侧面积为64,故表面积为92.92思想方法：转化与划归1.让学生经历几何体的侧面展开过程，体会空间问题平面化的思想。2.通过相关公式的学习，感受不同几何体侧面积公式时间的联系。1．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆台S圆台侧＝12(c1＋c2)l＝?(r1＋r2)lr1、r2—上、下底面半径c1、c2—上、下底面圆周长l—侧面母线长2.直棱柱、正棱锥、正棱台的侧面展开图及侧面积公式学习启示•理性的学习不是知道什么，而是怎样知道，过程的体验往往比结果更重要！