高中数学 简单线性规划问题2课件 新人教A版必修5 课件VIP免费

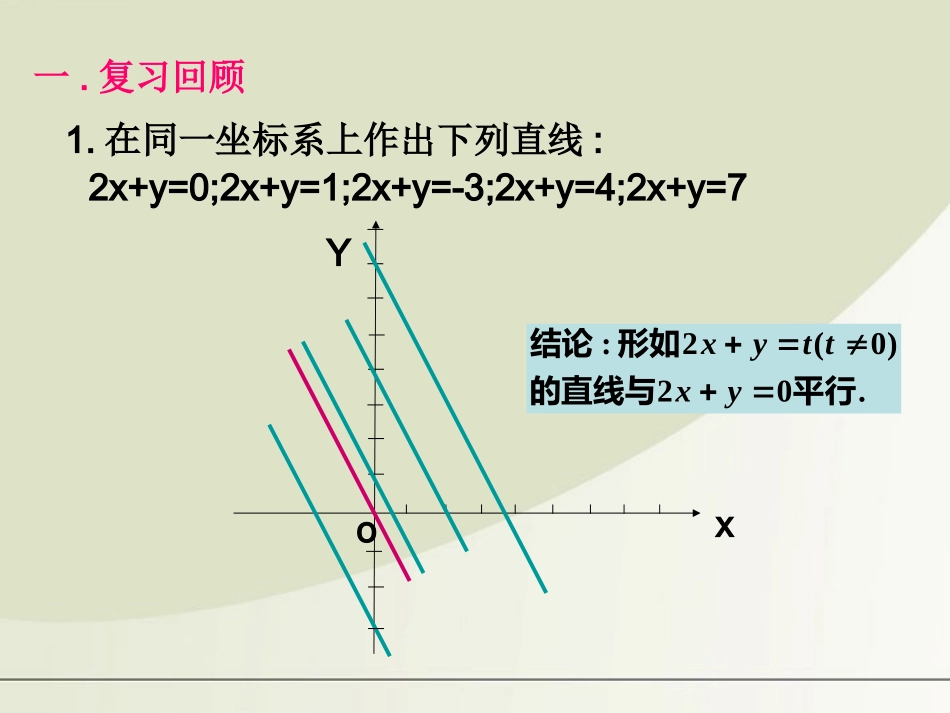
一.复习回顾1.在同一坐标系上作出下列直线:2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7.02)0(2:平行的直线与形如结论yxttyxxYo2.作出下列不等式组的所表示的平面区域1255334xyxyx55x=1x-4y+3=03x+5y-25=01ABCC:(1.00,4.40)A:(5.00,2.00)B:(1.00,1.00)Oxy问题1：x有无最大（小）值？问题2：y有无最大（小）值？问题3：2x+y有无最大（小）值？1255334xyxyx二.提出问题把上面两个问题综合起来:1255334xyxyx设z=2x+y,求满足时,求z的最大值和最小值.55x=1x-4y+3=03x+5y-25=01ABCC:(1.00,4.40)A:(5.00,2.00)B:(1.00,1.00)Oxy.1255334.1所表示的区域先作出xyxyx02yx02:.20yxl作直线Rttyxll,2:.30直线平行的作一组与直线直线L越往右平移,t随之增大.以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.3112,12252minmaxZZ1255334xyxyx设z=2x+y,求满足时,求z的最大值和最小值.线性目标函数线性约束条件线性规划问题任何一个满足不等式组的（x,y）可行解可行域所有的最优解有关概念由x，y的不等式(或方程)组成的不等式组称为x，y的约束条件。关于x，y的一次不等式或方程组成的不等式组称为x，y的线性约束条件。欲达到最大值或最小值所涉及的变量x，y的解析式称为目标函数。关于x，y的一次目标函数称为线性目标函数。求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。满足线性约束条件的解（x，y）称为可行解。所有可行解组成的集合称为可行域。使目标函数取得最大值或最小值的可行解称为最优解。三、课堂练习：2zxy1）求使的最大值，使x,y满足约束条件11yxxyy2）求使的最大值和最小值，使x,y满足约束条件35zxy5315153xyyxxy551Oxyy-x=0x+y-1=01-1y+1=0A(2,-1)B(-1,-1)3maxzmin3z551Oxy1-15x+3y=15X-5y=3y=x+1A(-2,-1)B(3/2,5/2)11;17minmaxZZ引例：某工厂用A、B两种配件生产甲、乙两种产品，每生产一件甲产品使用4个A配件耗时1h，每生产一件乙产品使用4个B配件耗时2h；该厂每天最多可从配件厂获得16个A配件和12个B配件，按每天工作8h计算，请你列出该厂的日生产安排满足的数学关系式，并在直角坐标系中画出相应的平面图形。若生产一件甲产品获利2万元，生产一件乙产品获利3万元，采用哪种生产安排利润最大？xy解：设甲、乙两种产品分别生产、件，由已知条件可得二元一次不等式组：2841641200xyxyxy（1）23zxy约束条件线性约束条件目标函数线性目标函数讲解（1）若不考虑实际意义，如何求z的最小值？（2）若生产一件甲产品获利3万元，生产一件乙产品获利2万元，如何安排生产才能获得最大利润？变式利用图解法解决线性规划问题的步骤：画——画出线性约束条件所表示的可行域答——做出答案求——根据观察的结论，先求交点的坐标，再求出最优解移——在目标函数所表示的一组平行线（与目标函数中z=0平行）中，利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线小结作业:P106习题A组第4题