高中数学 3.1函数的单调性与极值课件 北师大版选修1 1 课件VIP免费

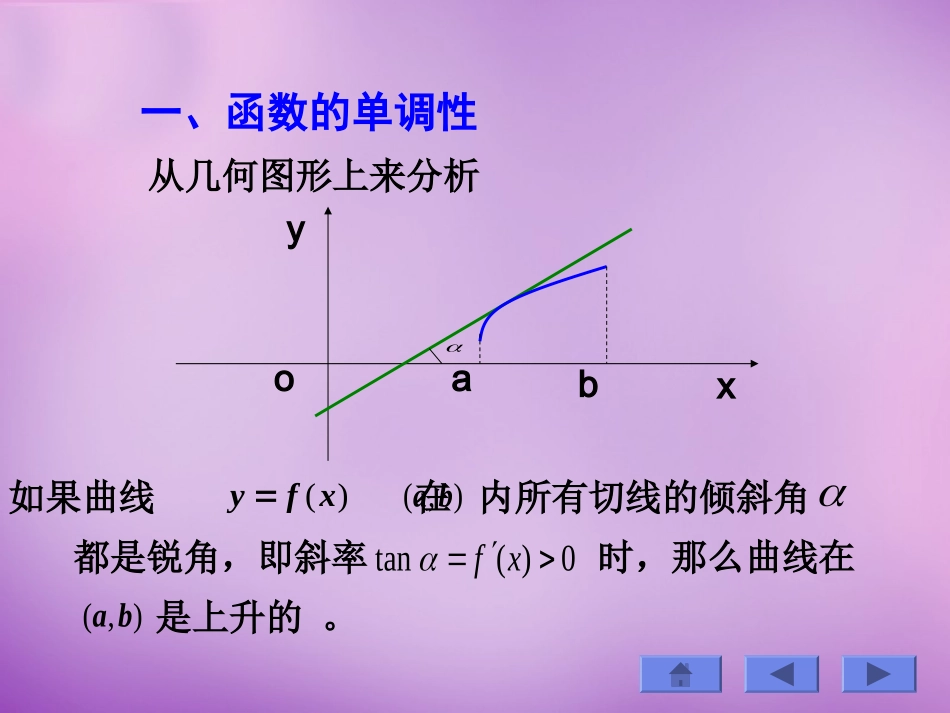
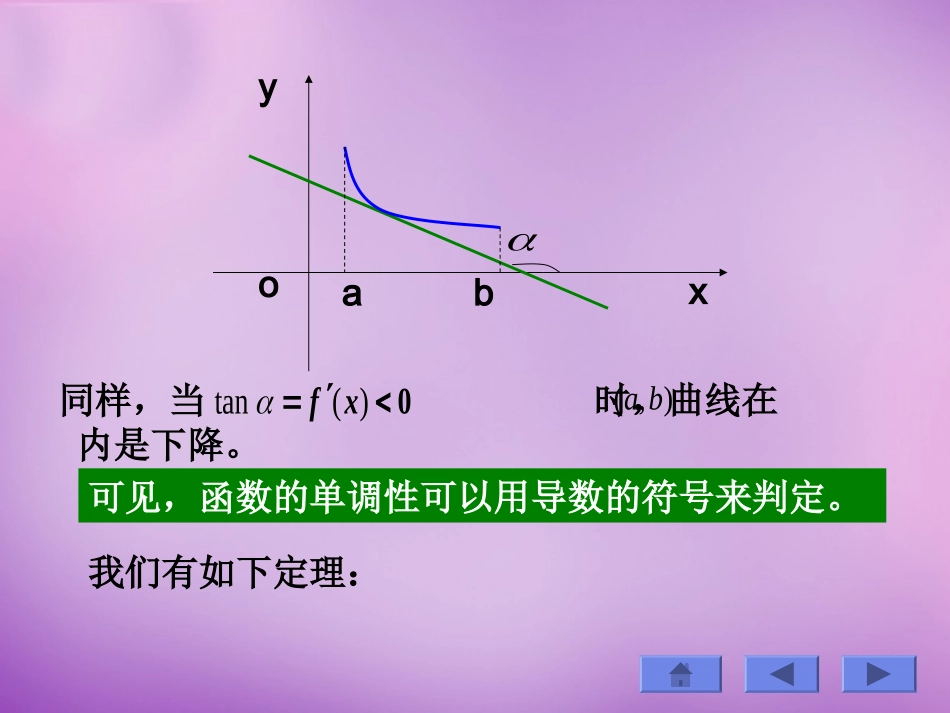
函数的单调性与极值一、函数的单调性二、函数的极值三、函数的最值一、函数的单调性从几何图形上来分析abxyo)(xfy),(ba都是锐角，即斜率0)(tanxf是上升的。),(ba如果曲线在内所有切线的倾斜角时，那么曲线在可见，函数的单调性可以用导数的符号来判定。aboyx同样，当时，曲线在内是下降。),(ba0)(tanxf我们有如下定理：定理1设函数在上连续，在区间),(ba)(xfyba,内可导，（1）如果在内，则在),(ba0)(xf)(xfba,上单调增加；),(ba0)(xf)(xfba,上单调减少。（2）如果在内，则在注意：（1）将定理中的闭区间换成其他各种区间定理的结论仍成立。ba,单调增加的充分条件，而不是必要条件。（2）在内，只是在上),(ba0)(xf)(xfba,考察函数3)(xxf，但等号只在个别处成立，（3）如果在区间内ba,0)(xf（或0)(xf）仍是单调增加（或单调减少）的。则函数在上)(xfba,考察函数3)(xxf例1判定函数的单调性。xxxfarctan)(解的定义域是。)(xf),(01111)(222xxxxf在区间和都有，只有当)0,(),0(0)(xf0x时，，所以在内单调减少。0)0(f)(xf),(例2求函数的单调区间。xxxf3)(3解的定义域是)(xf),()1)(1(333)(2xxxxf令，得，0)(xf1,1xx它们将定义域),(当时，)1,1(x0)(xf当时，。)1,(),1(x0)(xf所以的单调增加区间是和；单调递减区间是)(xf)1,(),1()1,1(例3确定函数的单调区间。23352353)(xxxf解的定义域是)(xf),()1,(),(11),1(分成三个区间令，得，又处导数不存在，0)(xf1x0x1x，这两点将分成三个区间，0x),(列表分析在各个区间的符号：)(xfx)0,()1,0(),(1)(xf)(xf331321)(xxxxxf由表可知，的单调增加区间为和)(xf)0,(，单调减少区间为。),1()1,0(二、函数的极值设函数在点的某邻域内有定义，)(xf0x1定义（1）如果对该领域内的任意点，都有)(xxx)()(0xfxf，则称是的极大值，称是)(0xf)(xf0x的极大值点。)(xf（2）如果对该领域内的任意点，都有)(xxx)()(0xfxf，则称是的极小值，称)(0xf)(xf0x是的极小值点。)(xf函数的极大值和极小值统称为极值，极大值点和极小致点统称为极值点。注意：极值是局部性的。因而，函数可以有许多个极大值和极小值，并且极大值不一定大于极小值。oxyab2极值存在的必要条件和充分条件定理2（极值的必要条件）如果函数在点)(xf处可导，且在点取得极值，则。0x0x0)(0xf定理2指出：可导函数的极值点必定是驻点。0)(0xf0x)(xf使的点称为函数得驻点。反过来，驻点不一定是极值点。3)(xxf考察函数另一方面，函数不可导的点也可能是极值点。0xxxf,)(考察函数定理3（极值的第一充分条件）设函数)(xf在点连续，且在点的某一空心邻域0x0x)0)(,(),(0000xxxx内可导。（1）如果在内，在),(00xx0)(xf),(00xx内，则函数在点处取极大值；0)(xf)(xf0x)(0xf（2）如果在内，在),(00xx0)(xf),(00xx内，则函数在点处取极小值；0)(xf)(xf0x)(0xf（3）如果在和内不变)(xf),(00xx),(00xx号，则在处无极值。)(xf0x定理3即：设在点的某一空心邻域内可导，)(xf0x当有小增大经过时，如果由正变负，x0x)(xf则是极大值点；如果由负变正，0x)(xf极小值点；如果则是0x)(xf不变号，则不是极值点。0x例4求函数的极值。1093)(23xxxxf解的定义域是)(xf),()3)(1(3963)(2xxxxxf令，得驻点。0)(xf3,121xx当时，11x0)(xf当时，31x0)(xf当时，。3x0)(xf)(xf3x在处取得极小值17)3(f例5求函数的极值。123)(32xxxf解的定义域是)(xf),(333111)(xxxxf令，得驻点，而时不存在。0)(xf1x0x)(xf由定理3知，在处取得极大值。)(xf11x15)1(f因此函数只可能在这两点取得极值，列表讨论如下：极大值1极小值x)(xf)(xf)0,()1,0(01...