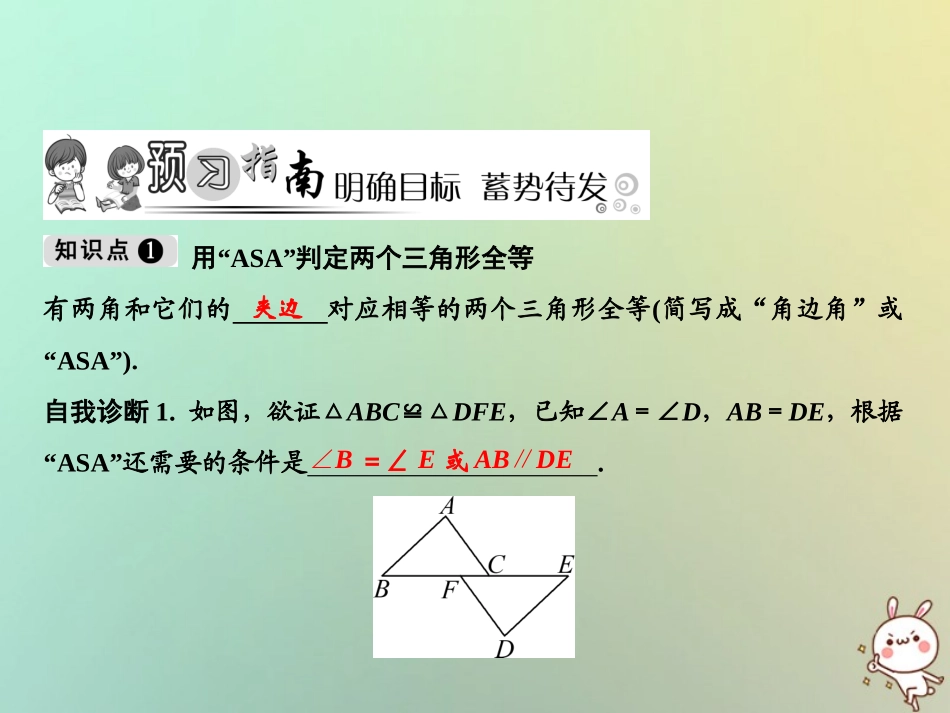
第十二章全等三角形12.2三角形全等的判定第3课时角边角、角角边2018秋季数学八年级上册•R用“ASA”判定两个三角形全等有两角和它们的对应相等的两个三角形全等(简写成“角边角”或“ASA”).自我诊断1.如图,欲证△ABC≌△DFE,已知∠A=∠D,AB=DE,根据“ASA”还需要的条件是.夹边∠B=∠E或AB∥DE用“AAS”判定两个三角形全等有两角和其中一角的对应相等的两个三角形全等(简写成“角角边”或“AAS”).对边自我诊断2.如图,用“AAS”直接判定△ACD≌△ABE,需要添加的条件是()A.∠ADC=∠AEB,∠C=∠BB.∠ADC=∠AEB,CD=BEC.AC=AB,AD=AED.AC=AB,∠C=∠BB易错点:在判定两个三角形全等时,一个三角形用“ASA”,另一个用“AAS”.自我诊断3.在△ABC和△DEF中,AB=EF,∠A=∠E=50°,∠B=75°,∠D=55°,则有()A.这两个三角形不可能全等B.这两个三角形可能不全等C.这两个三角形一定全等,且△ABC≌△EFDD.这两个三角形一定全等,且△ABC≌△EDFC1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是()A.甲B.乙C.甲和乙都是D.都不是B2.如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是()A.∠A=∠DB.AB=DCC.∠ACB=∠DBCD.AC=BD3.如图,已知:∠B=∠DEF,BC=EF,若要以“ASA”为依据证明△ABC≌△DEF,还缺条件;若要以“AAS”为依据,还缺条件.D∠ACB=∠F∠A=∠D4.如图,∠1=∠2,∠3=∠4,求证:AC=AD.证明:∵∠3=∠4,∴∠ABC=∠ABD,在△ABC和△ABD中,∠1=∠2,AB=AB,∠ABC=∠ABD,∴△ABC≌△ABD(ASA),∴AC=AD.5.如图,已知EC=AC,∠B=∠D,∠BCE=∠DCA.求证:BC=DC.证明:∵∠BCE=∠DCA,∴∠BCE+∠ECA=∠DCA+∠ECA,∴∠ACB=∠ECD,在△ABC和△EDC中,∠B=∠D∠ACB=∠ECDAC=EC,∴△ABC≌△EDC(AAS),∴BC=DC.6.如图所示,如果∠B=∠C,AB=DC,下列结论中,错误的是()A.AC=BDB.∠A=∠DC.OB=OCD.△AOB和△DOC不全等D7.在△ABC和△DEF中,已有条件AB=DE,还需要添两个条件才能使△ABC≌△DEF,不能添加的一组条件是()A.∠B=∠E,BC=EFB.BC=EF,AC=DFC.∠A=∠D,∠B=∠ED.∠A=∠D,BC=EFD8.如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSSB.SASC.AASD.ASAD9.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=.10.如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加一个条件为(答案不唯一,只需填一个).3∠B=∠E或∠A=∠D11.如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.证明:∵DE∥AB,∴∠BAC=∠ADE,在△ABC和△DAE中,∠B=∠DAEAB=DA∠BAC=∠ADE,∴△ABC≌△DAE(ASA),∴BC=AE.12.(泸州中考)如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.证明:∵AF=CD,∴AC=DF,∵BC∥EF,∴∠ACB=∠DFE,在△ABC和△DEF中,∠A=∠DAC=DF∠ACB=∠DFE,∴△ABC≌△DEF(ASA),∴AB=DE.13.在△ABO中,∠AOB=90°,AO=BO,直线MN经过点O,且AC⊥MN于C,BD⊥MN于D.(1)当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;(2)当直线MN绕点O旋转到图②的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明.解:(1)在图①中,∵△AOB中,∠AOB=90°,∴∠AOC+∠BOD=90°,直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,∴∠ACO=∠BDO=90°,∴∠AOC+∠OAC=90°,∴∠OAC=∠BOD,在△ACO和△ODB中,∠ACO=∠ODB=90°∠OAC=∠BODAO=OB,∴△ACO≌△ODB(AAS),∴OC=BD,AC=OD,∴CD=AC+BD;(2)图②:在△AOB中,∠AOB=90°,∴∠AOC+∠BOD=90°,直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,∴∠ACO=∠BDO=90°,∴∠AOC+∠OAC=90°,∴∠OAC=∠BOD,在△ACO和△ODB中,∠ACO=∠ODB=90°∠OAC=∠BODAO=OB,∴△ACO≌△ODB(AAS),∴OC=BD,AC=OD,∴CD=OC-OD=BD-AC,即CD=BD-AC.