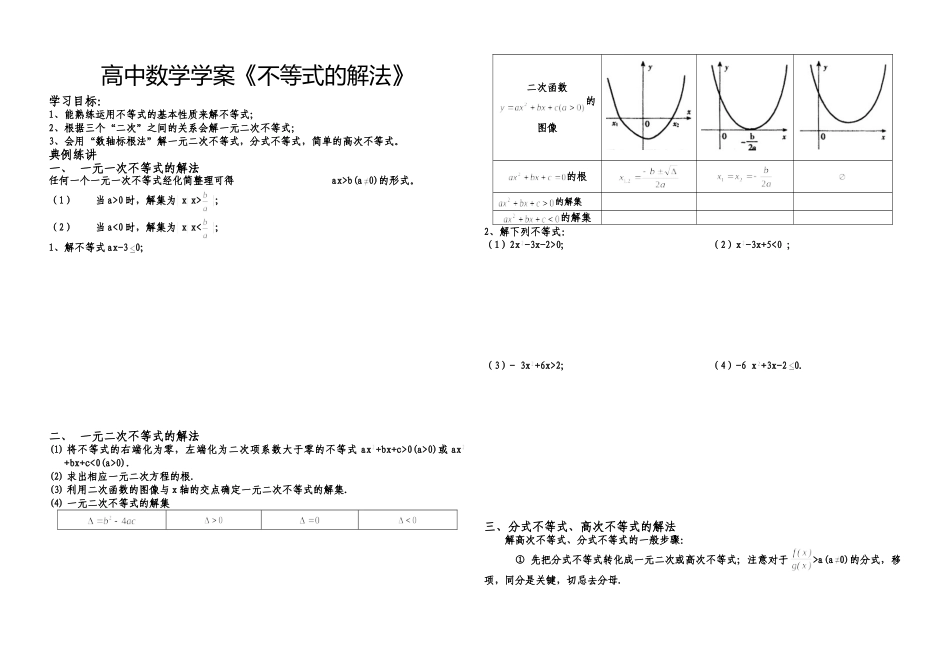
高中数学学案《不等式的解法》学习目标:1、能熟练运用不等式的基本性质来解不等式;2、根据三个“二次”之间的关系会解一元二次不等式;3、会用“数轴标根法”解一元二次不等式,分式不等式,简单的高次不等式。典例练讲一、 一元一次不等式的解法任何一个一元一次不等式经化简整理可得ax>b(a 0)的形式。(1)当 a>0 时,解集为 x x>;(2)当 a<0 时,解集为 x x<;1、解不等式 ax-3 0;二、 一元二次不等式的解法(1) 将不等式的右端化为零,左端化为二次项系数大于零的不等式 ax +bx+c>0(a>0)或 ax+bx+c<0(a>0).(2) 求出相应一元二次方程的根.(3) 利用二次函数的图像与 x 轴的交点确定一元二次不等式的解集.(4) 一元二次不等式的解集二次函数的图像的根的解集的解集2、解下列不等式:(1)2x -3x-2>0; (2)x -3x+5<0 ; (3)- 3x +6x>2; (4)-6 x +3x-2 0.三、分式不等式、高次不等式的解法 解高次不等式、分式不等式的一般步骤: ① 先把分式不等式转化成一元二次或高次不等式;注意对于>a(a 0)的分式,移项,同分是关键,切忌去分母.② 将不等式化为(x-x1)(x-x2)…(x-xn)>0(<0)形式,并将各因式 x 的系数化“+”;(为了统一方便)③ 求根,并在数轴上表示出来;③由右上方穿线,经过数轴上表示各根的点(为什么?);④ 若不等式(x 的系数化“+”后)是“>0”,则找“线”在 x 轴上方的区间;若不等式是“<0”,则找“线”在 x 轴下方的区间.注意:奇穿偶不穿例、解不等式:(x-2)2(x-3)3(x+1)<0.解:①检查各因式中 x 的符号均正;②求得相应方程的根为:-1,2,3(注意:2 是二重根,3是三重根);③在数轴上表示各根并穿线,每个根穿一次(自右上方开始),如下图:④∴原不等式的解集为:{x|-1