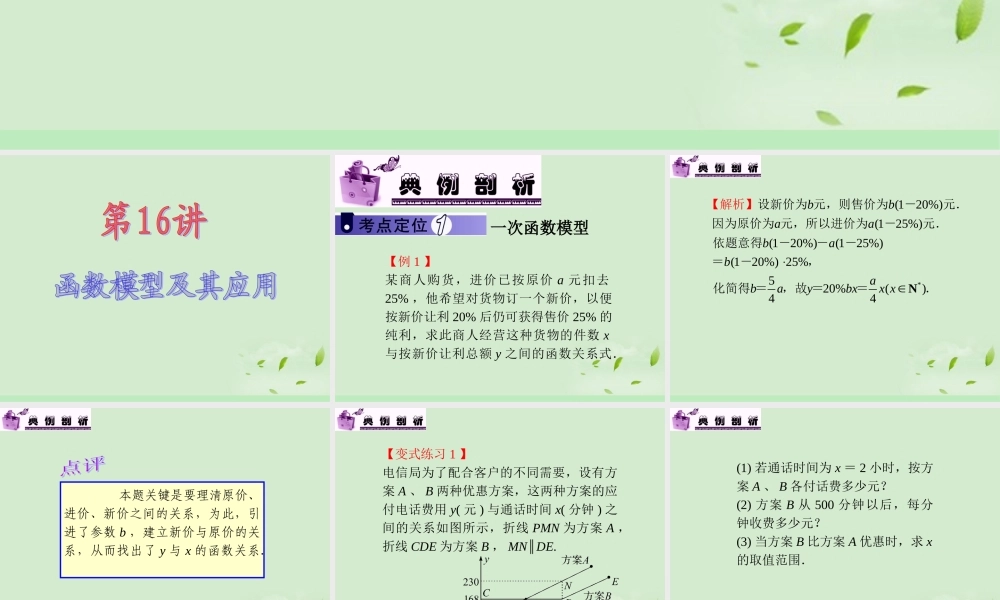
一次函数模型 【例 1 】某商人购货,进价已按原价 a 元扣去25% ,他希望对货物订一个新价,以便按新价让利 20% 后仍可获得售价 25% 的纯利,求此商人经营这种货物的件数 x与按新价让利总额 y 之间的函数关系式.*(120%)(125%)(120%)(125%)(120%) 25%520%()44bbaabababaybxx xN设新价为 元,则售价为-元.因为原价为 元,所以进价为-元.依题意得---=-,化简得 =,故 ==【解析】. 本题关键是要理清原价、进价、新价之间的关系,为此,引进了参数 b ,建立新价与原价的关系,从而找出了 y 与 x 的函数关系. 【变式练习 1 】电信局为了配合客户的不同需要,设有方案 A 、 B 两种优惠方案,这两种方案的应付电话费用 y( 元 ) 与通话时间 x( 分钟 ) 之间的关系如图所示,折线 PMN 为方案 A ,折线 CDE 为方案 B , MN∥DE.(1) 若通话时间为 x = 2 小时,按方案 A 、 B 各付话费多少元?(2) 方案 B 从 500 分钟以后,每分钟收费多少元?(3) 当方案 B 比方案 A 优惠时,求 x的取值范围. 60,98500,23098(060).380(60)10/ /168(0500).318(500)103120120120 80 11610120168.1ABABAMNxfxxxBMNDEfxxxxff方案 :,.得=方案 :由,得=当 =时,=+ =,=【解析】 (1)33(1) 18180.310105000.3880(168)388003880.382380()3BBABABfnfnnnBMNCDxffxffx因为+ -=+ +--=,所以方案 从分钟以后,每分钟收费元.由图可知,与的交点为,,所以,当时,;当时,故所求 的取值范围是,+.二次函数模型 【例 2 】某型号的电视机每台降价 x 成 (1 成为 10%) ,售出的数量就增加 mx 成, m∈R + .(1) 若某商场现定价为每台 a 元,售出量是 b 台,试建立降价后的营业额 y 与 x 的函数关系.问当m = 5/4 时,营业额增加 1.25% ,每台降价多少元?(2) 为使营业额增加,当 x = x0(0