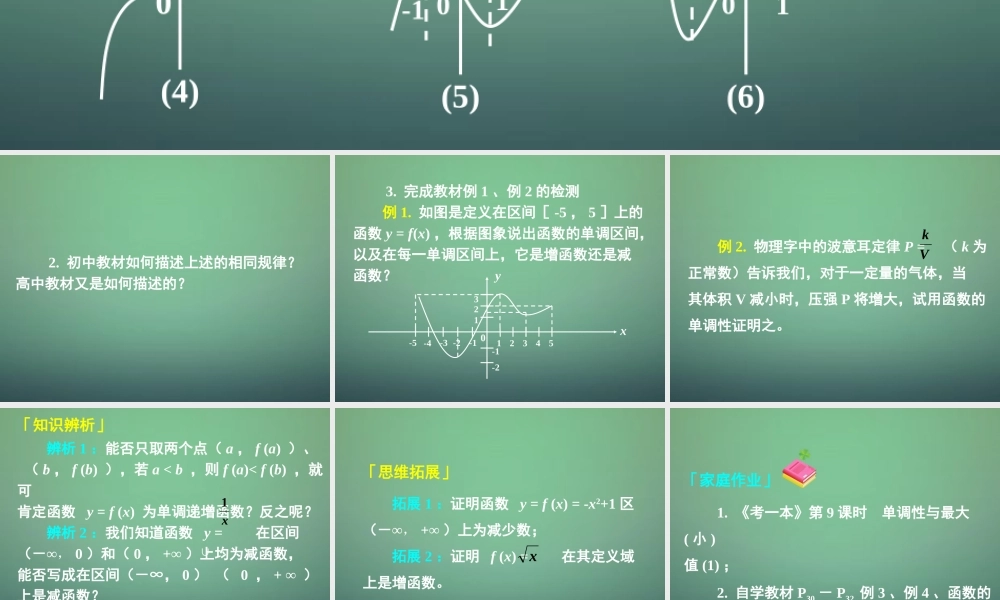
「自我感悟」 1. 分析下图中函数图象的变化规律,并将相同规律的图象部分绘制出来-12y0(1)xx=-2y(2)x00y(3)x0y(4)x0y(5)x-110y(6)x1-22 2. 初中教材如何描述上述的相同规律?高中教材又是如何描述的? 3. 完成教材例 1 、例 2 的检测 例 1. 如图是定义在区间[ -5 , 5 ]上的函数 y = f(x) ,根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?0-1-2-5 -4-354123y-1-2321x 例 2. 物理字中的波意耳定律 P = ( k 为正常数)告诉我们,对于一定量的气体,当其体积 V 减小时,压强 P 将增大,试用函数的单调性证明之。Vk「知识辨析」 辨析 1 :能否只取两个点( a , f (a) )、 ( b , f (b) ),若 a < b ,则 f (a)< f (b) ,就可肯定函数 y = f (x) 为单调递增函数?反之呢? 辨析 2 :我们知道函数 y = 在区间(-∞, 0 )和( 0 , +∞ )上均为减函数,能否写成在区间(-∞, 0 ) ( 0 , + ∞ )上是减函数? 辨析 3 :能否在函数 y = f (x) 的某个区间有最大值 ( 或最小值 ) 就能肯定该值为函数 y = f (x) 的最大值 ( 或最小值 ) ?x1∩「思维拓展」 拓展 1 :证明函数 y = f (x) = -x2+1 区(-∞, +∞ )上为减少数; 拓展 2 :证明 f (x) = 在其定义域上是增函数。x「家庭作业」 1. 《考一本》第 9 课时 单调性与最大( 小 )值 (1) ; 2. 自学教材 P30 - P32 例 3 、例 4 、函数的最值与单调性有怎样的关系?