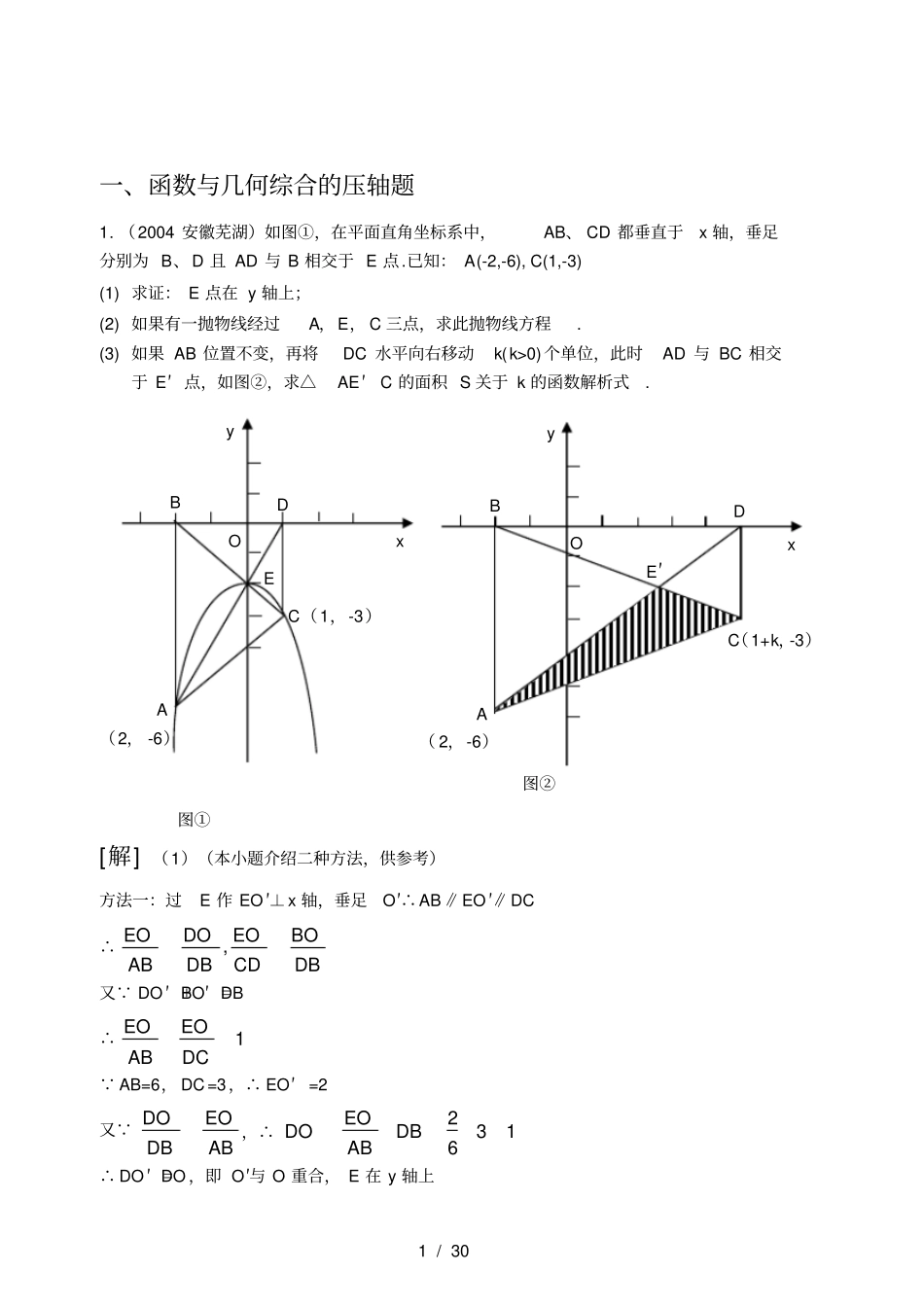
1 / 30 一、函数与几何综合的压轴题1. (2004 安徽芜湖)如图①,在平面直角坐标系中,AB、 CD 都垂直于x 轴,垂足分别为 B、D 且 AD 与 B 相交于 E 点.已知: A(-2,-6), C(1,-3) (1) 求证: E 点在 y 轴上;(2) 如果有一抛物线经过A,E, C 三点,求此抛物线方程. (3) 如果 AB 位置不变,再将DC 水平向右移动k(k>0)个单位,此时AD 与 BC 相交于 E′ 点,如图②,求△AE′C 的面积 S 关于 k 的函数解析式. [解] (1)(本小题介绍二种方法,供参考)方法一:过E 作 EO ′⊥x 轴,垂足O′∴AB∥EO ′∥DC∴,EODOEOBOABDBCDDB又 DO ′ +BO′ =DB∴1EOEOABDC AB=6, DC =3,∴ EO′=2又 DOEODBAB,∴2316EODODBAB∴ DO ′ =DO ,即 O′与 O 重合, E 在 y 轴上图①C(1,-3)A (2, -6)B D O x E y 图②C(1+k,-3)A ( 2,-6)B D O x E′y 2 / 30 方法二:由D(1, 0), A(-2, -6),得 DA 直线方程: y=2x-2①再由 B(-2,0), C(1,-3),得 BC 直线方程: y=-x-2 ②联立①②得02xy∴ E 点坐标( 0,-2),即 E 点在 y 轴上( 2)设抛物线的方程y=ax2+bx+c(a≠ 0)过 A(-2,-6), C(1,-3)E( 0,-2)三点,得方程组42632abcabcc解得 a=-1, b=0,c=-2 ∴抛物线方程y=- x2-2 ( 3)(本小题给出三种方法,供参考)由( 1)当 DC 水平向右平移k 后,过 AD 与 BC 的交点 E′作 E′F⊥x 轴垂足为F。同( 1)可得:1E FE FABDC得: E′F=2 方法一:又 E′F∥ ABE FDFABDB,∴13DFDBS△AE′C= S△ ADC- S△E′DC= 11122223DCDBDCDFDCDB???= 13DCDB?=DB=3+ kS=3+k 为所求函数解析式方法二: BA∥DC ,∴ S△ BCA=S△ BDA∴ S△AE ′C= S△ BDE′11 32322BDE Fkk?∴ S=3+k 为所求函数解析式. 证法三: S△ DE′C∶ S△AE ′C=DE ′∶AE′ =DC ∶AB=1∶2 同理: S△DE′C∶ S△DE ′B=1∶ 2,又 S△DE ′C∶S△ABE ′=DC 2∶AB2=1∶ 4 ∴2213992AE CABCDSSABCDBDk?梯形∴ S=3+k 为所求函数解析式. 2. (2004 广东茂名)已知:如图,在直线坐标系中,以点M (1, 0)为圆心、直3 / 30 径 AC 为22的圆与 y 轴交于 A、D 两点 . ( 1)求点 A 的坐标;( 2)设过点A 的直线 y= x+b 与 x 轴交于点B.探究:直线AB 是否⊙...