数学 第四章 导数应用 4.1.1 导数与函数的单调性(2)课件 北师大版选修1 1 课件VIP免费

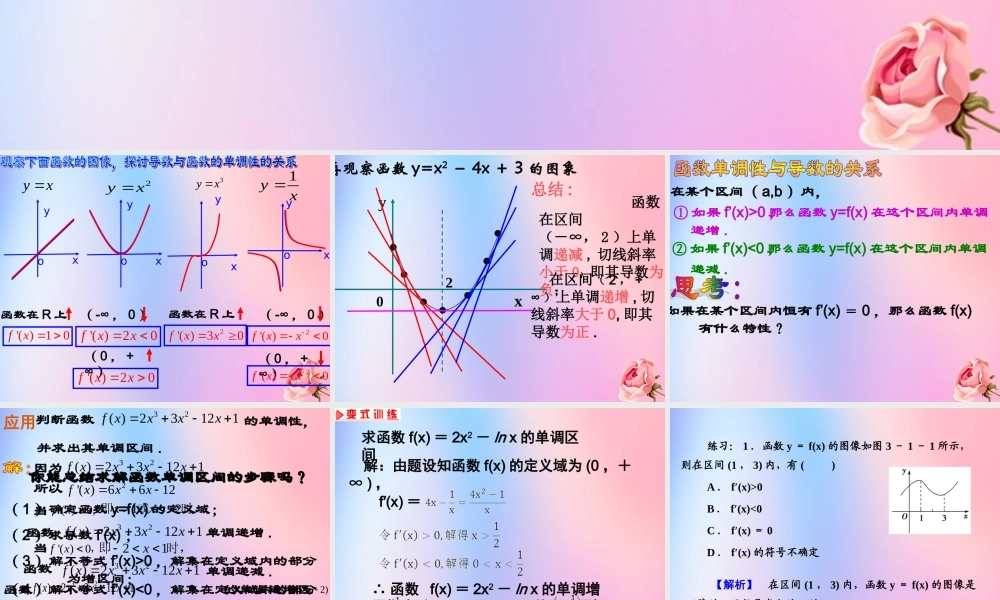
§1 函数的单调性与极值1 ． 1 导数与函数的单调性yoxxyoxyoxy1yx2yx3yx函数在 R 上'( )10fx  （ -∞ ， 0 ）（ 0 ， +∞ ）'( )20fxx'( )20fxx函数在 R 上2'( )30fxx（ -∞ ， 0 ）2'( )0fxx（ 0 ， +∞ ）2'( )0fxxyox2yx0.......再观察函数 y=x2 － 4x ＋ 3 的图象 函数在区间（－∞， 2 ）上单调递减 , 切线斜率小于 0, 即其导数为负；总结 : 在区间（ 2 ， +∞ ）上单调递增 , 切线斜率大于 0, 即其导数为正 .在某个区间（ a,b ）内，① 如果 f’(x)>0 ，② 如果 f’(x)<0 ，那么函数 y=f(x) 在这个区间内单调 递增 .那么函数 y=f(x) 在这个区间内单调 递减 .如果在某个区间内恒有 f’(x) ＝ 0 ，那么函数 f(x) 有什么特性？判断函数32( )23121f xxxx的单调性，并求出其单调区间 .你能总结求解函数单调区间的步骤吗？你能总结求解函数单调区间的步骤吗？（ 1 ）确定函数 y=f(x) 的定义域；（ 2 ）求导数 f’(x) ；（ 3 ）解不等式 f’(x)>0 ，解集在定义域内的部分 为增区间；（ 4 ）解不等式 f’(x)<0 ，解集在定义域内的部分为减区间．因为32( )23121f xxxx所以2'( )6612fxxx当12即或时，xx 函数32( )23121f xxxx 单调递增 .当21即时，x函数32( )23121f xxxx单调递减 .'( )0,fx '( )0，fx 函数 的单调递增区间为单调递减区间为（ -2 ， 1 ）32( )23121f xxxx(1)(, 2)  ，和应用求函数 f(x) ＝ 2x2 － ln x 的单调区间 解：由题设知函数 f(x) 的定义域为 (0 ，＋∞ ) ，f′(x) ＝∴ 函数 f(x) ＝ 2x2 － ln x 的单调增区间为 ，单调减区间为 .练习： 1 ．函数 y ＝ f(x) 的图像如图 3 － 1 － 1 所示，则在区间 (1 ， 3) 内，有 ( )A ． f′(x)>0B ． f′(x)<0C ． f′(x) ＝ 0D ． f′(x) 的符号不确定【解析】 在区间 (1 ， 3) 内，函数 y ＝ f(x) 的图像是下降的，函数是减少的，则 f′(x)<0.答案 B2 ．函数 y ＝ x － ex 的递增区间为 ( )A ． (1 ，＋∞ ) B ． (0 ，＋∞ )C ． ( －∞， 0) D ． ( －∞，1)【解析】 y′ ＝ 1 － ex ，令 y′>0 ，得 ex<1 ＝ e0 ，解得 x<0.答案 C3 ． y ＝ x ＋ sin x 在 [0 ， π) 上是 ________( 填增加的或减少的 ) ．【解析】 y′ ＝ 1 ＋ cos x ，∵ 0≤x<π ，∴－ 10 ，∴y ＝ x ＋ sin x 在 [0 ， π) 上是增加的．【答案】 增加的设 是函数 的导函数， 的图象如右图所示 , 则 的图象最有可能的是 ( )( )f x'( )fx'( )yfx( )yf xxyo12( )yf xxyo12( )yf x(A)(B)xyo12( )yf xxyo1 2( )yf x(C)(D)xyo'( )yfx2高考链接课堂补充练习求下列函数的单调区间x323)e(x(3)yx3x(2)y45x2x(1)y