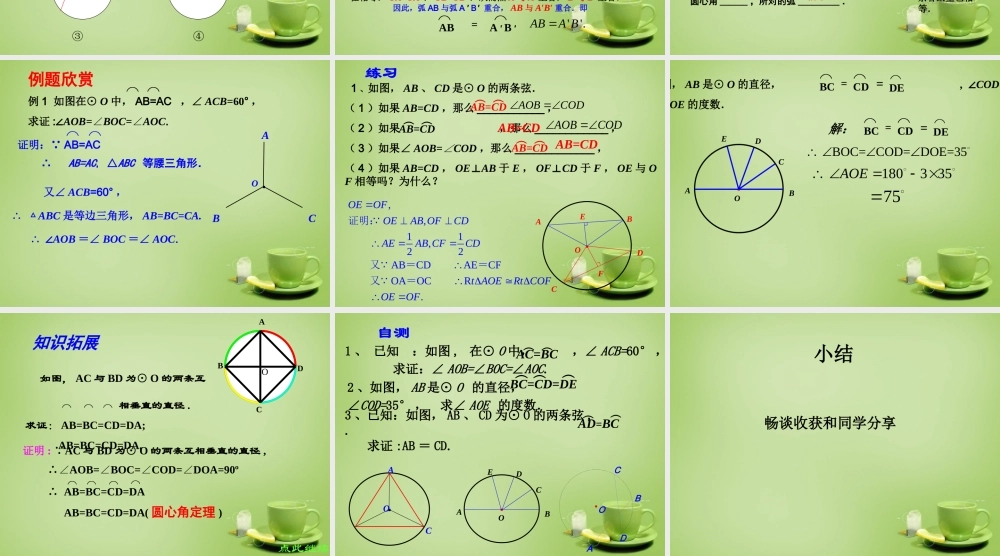
24.1.3 弧、弦、圆心角1 、理解圆的旋转不变性 2 、了解圆心角的概念。 3 、掌握圆心角、弧和弦的关系定理及推论。学习目标圆是中心对称图形吗 ? 它的对称中心在哪里 ?·思考圆是中心对称图形,它的对称中心是圆心 .· 圆心角:我们把顶点在圆心的角叫做圆心角 .OBA如图中所示, ∠ AOB 就是一个圆心角。定义判别下列各图中的角是不是圆心角,并说明理由。①②③④ 如图,将圆心角∠ AOB 绕圆心 O 旋转到∠ A’OB’ 的位置,你能发现哪些等量关系?为什么?根据旋转的性质,将圆心角∠ AOB 绕圆心 O 旋转到∠ A′OB′ 的位置时,显然∠ AOB =∠ A′OB′ ,射线 OA 与 OA′ 重合, OB 与 OB′ 重合.而同圆的半径相等, OA=OA′ , OB=OB′ ,从而点 A 与 A′ 重合, B 与 B′ 重合.·OAB·OABA′B′A′B′探究''.ABA B因此,弧 AB 与弧 A ′ B ′ 重合, AB 与 A′B′ 重合.即⌒AB⌒A ′ B ′=同样,还可以得到:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角 _____ , 所对的弦 ________ ;在同圆或等圆中,如果两条弦相等,那么他们所对的圆心角 ______ ,所对的弧 _________ .这样,我们就得到下面的定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.相等相等相等相等同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.定理证明: AB=AC∴ AB=AC, △ABC 等腰三角形.又∠ ACB=60° , ∴△ ABC 是等边三角形, AB=BC=CA. ∴ ∠AOB =∠ BOC =∠ AOC.·ABCO例题欣赏例 1 如图在⊙ O 中, AB=AC ,∠ ACB=60° ,求证 :∠AOB=∠BOC=∠AOC.⌒ ⌒⌒ ⌒ 1 、如图, AB 、 CD 是⊙ O 的两条弦.( 1 )如果 AB=CD ,那么 ___________ ,( 2 )如果 ,那么 ____________ ,( 3 )如果∠ AOB=COD∠,那么 _____________ ,( 4 )如果 AB=CD , OE⊥AB 于 E , OF⊥CD 于 F , OE 与 OF 相等吗?为什么?·CABDEFOAOBCODAB=CDAOBCOD,,11,22ABCDAECFOAOCR.OEOFOEAB OFCDAEAB CFCDt AOERt COFOEOF证明: 又= = 又= AB=CD练习AB=CD︵︵AB=CD︵ ︵AB=CD︵︵2. 如图, A...