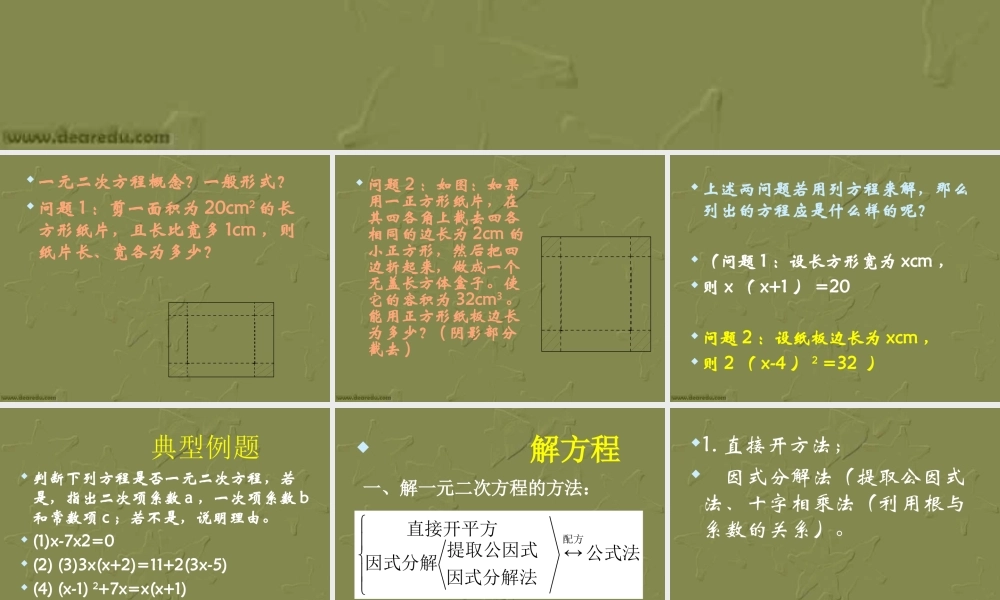
一元二次方程复习一元二次方程概念?一般形式?问题 1 :剪一面积为 20cm2的长方形纸片,且长比宽多 1cm ,则纸片长、宽各为多少? 问题 2 :如图:如果用一正方形纸片,在其四各角上截去四各相同的边长为 2cm 的小正方形,然后把四边折起来,做成一个无盖长方体盒子。使它的容积为 32cm3。能用正方形纸板边长为多少? ( 阴影部分截去 ) 上述两问题若用列方程来解,那么列出的方程应是什么样的呢?(问题 1 :设长方形宽为 xcm ,则 x ( x+1 ) =20问题 2 :设纸板边长为 xcm ,则 2 ( x-4 ) 2 =32 ) 典型例题 判断下列方程是否一元二次方程,若是,指出二次项系数 a ,一次项系数 b和常数项 c ;若不是,说明理由。 (1)x-7x2=0 (2) (3)3x(x+2)=11+2(3x-5) (4) (x-1) 2+7x=x(x+1) (5)y2 = - 4 解方程一、解一元二次方程的方法:公式法因式分解法提取公因式因式分解直接开平方配方 1. 直接开方法; 因式分解法(提取公因式法、十字相乘法(利用根与系数的关系)。 2. 配方法:( 1 )解完全的一元二次方程 ax2+bx+c=0(a≠0 , b≠0 , c≠0) 可以转化为适合于直接开平方法的形式 (x+m)2=n;(2) 记住配方的关键是“添加的常数项等于一次项系数一半的平方”;(3) 在数学思想方法方面,体会“转化”的思想和掌握配方法。 典型例题: x2 -8x-9=0. 解:移项,得 x 2-8x=9, 两边都加一次项系数一半的平方, x 2-8x+4 2=q+4 2, 配方,得 (x-4) 2=25, 解这个方程,得 x-4=±5 , 移项,得 x=4±5. 即 x 1=9,x2 =-1. ( 口头检验,是不是原方程的根 ) 3.用配方法解一元二次方程的步骤 (1) 化二次项系数为 1 ; (2) 移项,使方程左边只有二次项及一次项; (3) 在方程两边都加上一次项系数一半的平方; (4) 变形为 (x+m2)=n 的形式,如果 n≥0 ,得 x+m=± ,x=-m± .所以 x1=-m+ ,x2=-m-- 典型例题: (1)x2-10x+24=0; (2)x2-8x+15=0; (3)x2+2x-99=0; (4)y2+5y+2=0; (5)3x2-1=4x; (6)2x2+2x-30=0;(7)x2+px+q=0 (p2-4q≥0) ; 公式法:aacbbx242 强调公式的条件:04,02acba 根与系数关系abxxacxx2121 1. 应用一元二次方程的根与系数关系时,首先要把已知方程化成一般形式 .2. 应用一元二次方程的根与系数关系时,要特别注意,方程有实根的条件,即在初中代数里,当且仅当 b2-4ac≥0 时,才能应用根与系关系 .3. 可以通过一元二次方程系数判断方程根的情况 .