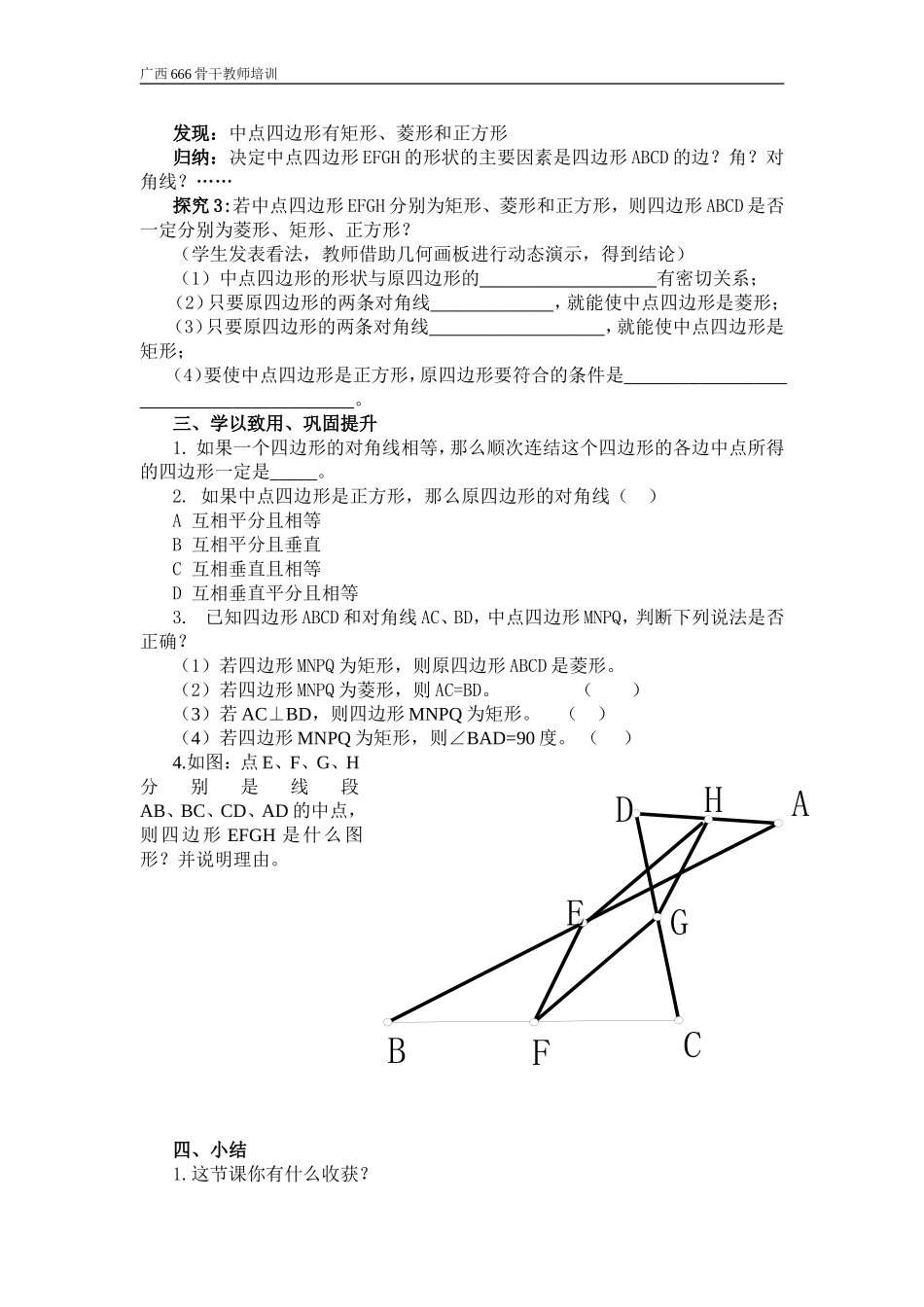
广西 666 骨干教师培训《课题:探究中点四边形》教学设计 陶源泉教学目标:1.知识与技能:(1)了解中点四边形的概念;(2)利用三角形中位线定理证明中点四边形是平行四边形,理解特殊的平行四边形的中点四边形的特征;(3)理解中点四边形的形状与原四边形的对角线的关系。 2. 过程与方法:(1)经历观察、猜想、证明中点四边形是平行四边形的过程熟练运用三角形中位线定理;(2)经历由一般到特殊的思维进程,发现并证明特殊的平行四边形的中点四边形的特征;3.情感态度与价值观:(1)通过数学活动培养学生观察、猜想、证明的探索精神;(2)通过小组讨论活动,培养学生合作的意识。 教学重点:1.任意四边形的中点四边形形状的判定和证明;2.特殊平行四边形的中点四边形形状的判定和证明。教学难点:影响中点四边形形状的主要因素的分析和概括。教学过程:一、复习旧知,情境引入1.回顾三角形中位线性质定理。2.探究1:出示问题:一块白铁皮零料形状如图,工人师傅要从中裁出一块平行四边形白铁皮,并使四个顶点分别落在原白铁皮的四条边上,可以如何裁?(学生思考、讨论、分析,想出解决办法)师:你能证明吗?生:已知:如图,点 E、F、G、H 分别是四边形 ABCD 各边中点。求证:四边形 EFGH 为平行四边形。(学生可连接 AC,也可连接 AC、BD)二、探索活动1.中点四边形的定义:顺次连接四边形各边中点所得的四边形叫做中点四边形。2.结合引例得出结论:任意一个四边形的中点四边形,都为平行四边形。探究2:若四边形 ABCD 分别为平行四边形、矩形、菱形、正方形,那它们的中点四边形会是什么形状呢?(四人小组探究一个特殊的四边形,说出中点四边形的形状并说明理由)在探究 1 的基础上,改变四边形 ABCD 的形状,使四边形 ABCD 分别为平行四边形、矩形、菱形、正方形,研究中点四边形 EFGH 形状。ABCDEFGH广西 666 骨干教师培训发现:中点四边形有矩形、菱形和正方形归纳:决定中点四边形 EFGH 的形状的主要因素是四边形 ABCD 的边?角?对角线?……探究 3:若中点四边形 EFGH 分别为矩形、菱形和正方形,则四边形 ABCD 是否一定分别为菱形、矩形、正方形?(学生发表看法,教师借助几何画板进行动态演示,得到结论)(1)中点四边形的形状与原四边形的 有密切关系;(2)只要原四边形的两条对角线 ,就能使中点四边形是菱形;(3)只要原四边形的两条对角线 ,就能使中点四边形是矩形;(4)要使中点四边形是正方...