数学苏教版选修1-1 导数的几何意义ppt 课件VIP免费

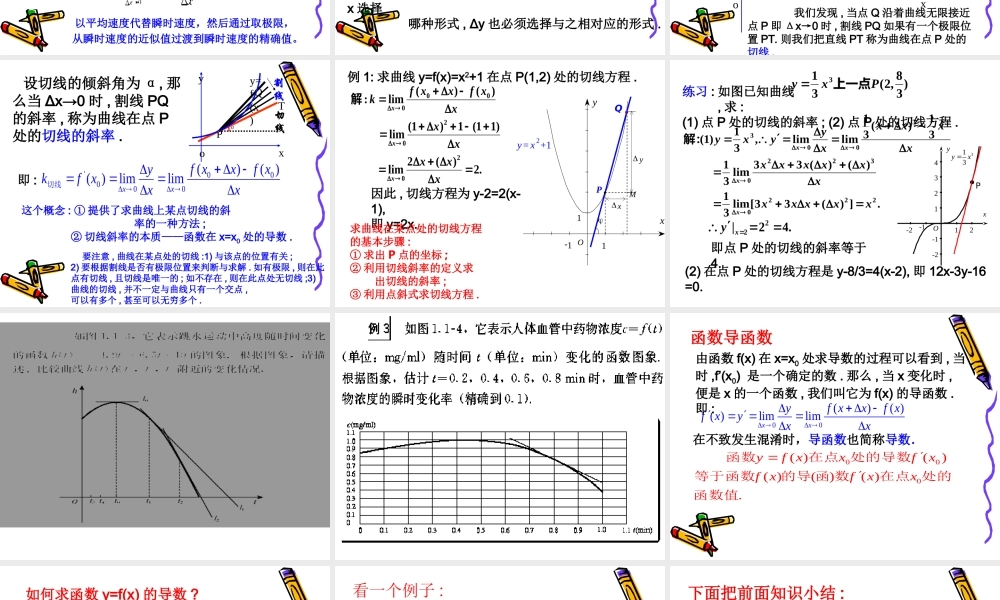
导数的几何意义 回顾① 平均变化率fx121)()f xxx2f(x函数 y=f(x) 的定义域为 D,x1.x2∈D,f(x) 从 x1 到x2 平均变化率为 :② 割线的斜率OABxyY=f(x)x1x2f(x1)f(x2)x2-x1= x△f(x2)-f(x1)= y△fkx121)()f xxx2f(x 回顾以平均速度代替瞬时速度，然后通过取极限，从瞬时速度的近似值过渡到瞬时速度的精确值。我们把物体在某一时刻的速度称为瞬时速度 .从函数 y=f(x) 在 x=x0 处的瞬时变化率是 :         1234nnTLLLLL1234limnLLLLLn  L 回顾以平均速度代替瞬时速度，然后通过取极限，从瞬时速度的近似值过渡到瞬时速度的精确值。我们把物体在某一时刻的速度称为瞬时速度 .从函数 y=f(x) 在 x=x0 处的瞬时变化率是 : 由导数的意义可知 , 求函数 y=f(x) 在点 x0处的导数的基本方法是 :00(1)()();yf xxf x  求函数的增量00()()(2);f xxf xyxx求平均变化率00(3)()lim.xyfxx 取极限，得导数注意 : 这里的增量不是一般意义上的增量 , 它可正也可负 . 自变量的增量 Δx 的形式是多样的 , 但不论 Δx 选择 哪种形式 , Δy 也必须选择与之相对应的形式 .回顾 PQoxyy=f(x)割线切线T导数的几何意义 : 我们发现 , 当点 Q 沿着曲线无限接近点 P 即 Δx→0 时 , 割线 PQ 如果有一个极限位置 PT. 则我们把直线 PT 称为曲线在点 P 处的切线 . 设切线的倾斜角为 α, 那么当 Δx→0 时 , 割线 PQ的斜率 , 称为曲线在点 P处的切线的斜率 .即 :'00000()()()limlimxxf xxf xykf xxx  切线这个概念 : ① 提供了求曲线上某点切线的斜 率的一种方法 ; ② 切线斜率的本质——函数在 x=x0 处的导数 . 要注意 , 曲线在某点处的切线 :1) 与该点的位置有关 ;2) 要根据割线是否有极限位置来判断与求解 . 如有极限 , 则在此点有切线 , 且切线是唯一的 ; 如不存在 , 则在此点处无切线 ;3)曲线的切线 , 并不一定与曲线只有一个交点 ,可以有多个 , 甚至可以无穷多个 .PQoxyy=f(x)割线切线T例 1: 求曲线 y=f(x)=x2+1 在点 P(1,2) 处的切线方程 .QPy= x 2+1xy-111OM yx.2)(2lim)11(1)1(lim)()(lim:2020000...